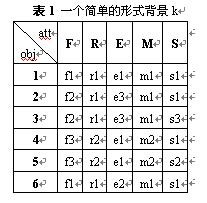
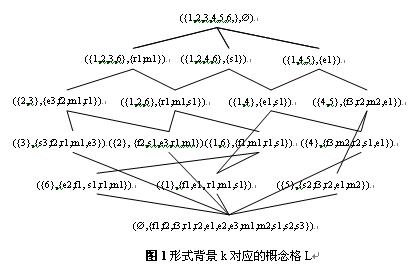
概念格(Concept Lattice)是一個以概念為元素的偏序集,它可以通過Hasse圖可視化,其中每個節點是一個概念。概念格結構模型來源於形式概念分析(FCA)理論,是FCA中的核心數據分析工具,它本質上描述了對象(樣本)與屬性(特徵)之間的關聯。
基本介紹
- 中文名:概念格
- 外文名:Concept Lattice
- 性質:構成伽羅瓦連線
- 形式:核心數據結構
- 別稱:形式概念分析
- 套用:信息檢索、數字圖書館等
概念格簡介
基本定理

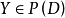
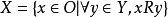

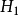
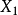
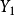
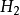
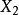


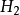



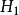
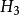
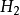
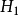
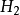
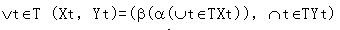
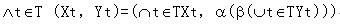
研究方向





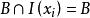

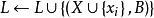
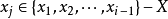
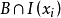
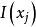
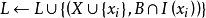
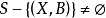
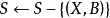
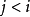



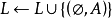
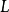
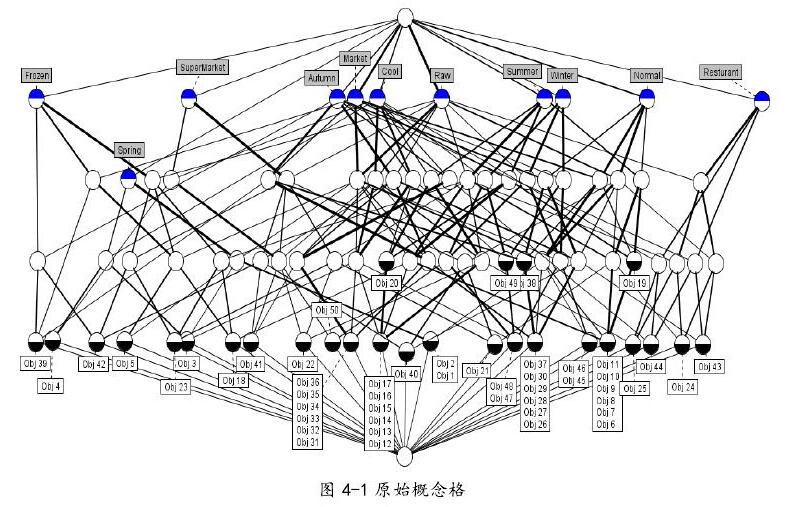
概念格(Concept Lattice)是一個以概念為元素的偏序集,它可以通過Hasse圖可視化,其中每個節點是一個概念。概念格結構模型來源於形式概念分析(FCA)理論,是FCA中的核心數據分析工具,它本質上描述了對象(樣本)與屬性(特徵)之間的關聯。

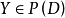
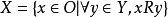

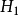
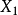
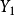
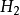
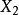


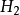

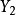




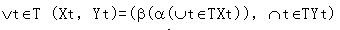
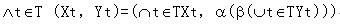



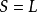


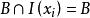

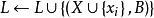
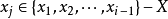
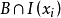
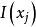
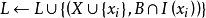
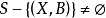
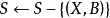
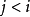
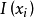

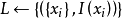

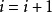

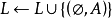
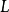
概念格(Concept Lattice)是一個以概念為元素的偏序集,它可以通過Hasse圖可視化,其中每個節點是一個概念。概念格結構模型來源於形式概念分析(FCA)理論,是FCA中的核心...
內容簡介 本書全面介紹了面向對象概念格的屬性約簡、特別是基於並不可約元和基於並可約元的面向對象概念格屬性約簡方法;面向對象概念格的壓縮;合成背景的面向對象...
正規概念分析是個非監督式機器學習技巧和資料分析方法。透過正規概念分析建立一個概念點陣,可以將所有的正規概念組織起來。這個點陣是由一群"自然"物件和"自然"屬性...
形式概念分析(Formal Concept Analysis,FCA)是Wille提出的一種從形式背景進行數據分析和規則提取的強有力工具,形式概念分析建立在數學基礎之上,對組成本體的概念、...
概念認知學習是一個新興的交叉研究領域,它由形式概念分析,粗糙集,粒計算,認知計算等理論聯合誘導出來。近年來,在大數據環境下概念認知學習表現出諸多的認知優勢。...
《人工智慧形式概念系統》是2011年科學出版社出版的圖書,作者是危輝。...... .2.2.3概念格2.2.4本體2.3心理學對此問題的研究2.4心理學對長時記憶的研究...
米據生,河北師範大學學術帶頭人,數學與信息科學學院院長、教授、碩士生和博士生導師、理學博士、香港中文大學博士後,主要從事概念格和粒計算的理論及其在地理信息系統中...
從事數學和信息科學的教學與研究工作,主要研究方向:粗糙集、概念格、隨機集、粒計算、數據挖掘和信息融合。 [1] 中文名 吳偉志 國籍 中國 出生日期 1964年3月 ...
[2] 基於加權和約束概念格的數據挖掘方法與天體光譜數據挖掘技術(60773014),國家自然科學基金,2008.1-2010.12,(已結題)[3] 基於數據格線的分散式數據挖掘方法...
2.基於領域本體的概念格的語義匹配研究, 四川省人事廳,2008.01-2009.12, 項目負責人。3.基於形式概念的用戶查詢與網頁匹配方法研究, 四川省教育廳自然重點, ...
Eclat算法是一種深度優先算法,採用垂直數據表示形式,在概念格理論的基礎上利用基於前綴的等價關係將搜尋空間(概念格)劃分為較小的子空間(子概念格)。...
決策形式背景(Formal decision context),由形式背景(Formal context)附加決策屬性得到,見專著《基於粗糙集的不確定決策》以及論文《決策形式背景的概念格屬性約簡》,...
