極分解定理

基本介紹

• 中文名：極分解定理
• 外文名：Polar decomposition theorem
• 別稱：乘法分解定理

極分解定理又稱乘法分解定理，它表示，任一可逆的二階張量F具有下列兩個唯一的相乘分解：

F=R·U或F_lL=R_lM·U_ML(右分解)

和F=V·R或F_lL=V_lm·R_mL(左分解)

式中為R正交張量，而U和V為對稱正定張量。下列關係成立：

U=(F^T·F)^1/2，

V=(F·F^T)^1/2，

式中F^T為F的轉置。
若把極分解定理套用於變形梯度F，則R為表示純轉動的轉動張量，而U和V分別為表示純變形的右和左伸長張量。在這種情況下，右分解表示首先進行純變形U，然後再進行轉動R，從而得到變形梯度F；而左分解則表示首先進行轉動R，然後再進行純變形V，從而得到變形梯度F。U和V是一個平方根張量。一般用分析方法求解張量的平方根是不容易的，但是關係

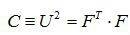
和

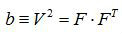
是容易由F求得的。C和b分別稱為右和左柯西-格林張量（見應變張量）。類似地，把極分解定理套用於相對變形梯度F_t，則有：

，

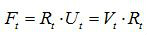
式中R_t為相對轉動張量，而U_t和V_t分別為右和左相對伸長張量。於是

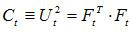
和

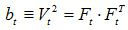
分別稱為右和左相對柯西-格林張量。