北宋人賈憲約1050年首先使用“賈憲三角”進行高次開方運算。
13世紀中國宋代數學家楊簫在《詳解九章算術》里討論這種形式的數表,並說明此表引自11世紀前半賈憲的《釋鎖算術》,並繪畫了“古法七乘方圖”。故此,楊輝三角又被稱為“賈憲三角”。
基本介紹
- 中文名:楊簫三角形
- 朝代:北宋
- 出處:《詳解九章算術》
- 別稱:賈憲三角
- 類型:數學
性質
1、每行數字左右對稱,由1開始逐漸變大,然後變小,回到1。
2、第n行的數字個數為n個。
3、第n行數字和為2^(n-1)。
4、每個數字等於上一行的左右兩個數字之和。可用此性質寫出整個帕斯卡三角形。
5、將第2n+1行第1個數,跟第2n+2行第3個數、第2n+3行第5個數……連成一線,這些數的和是第2n個斐波那契數。將第2n行第2個數,跟第2n+1行第4個數、第2n+2行第6個數……這些數之和是第2n-1個斐波那契數。
6、第n行的第1個數為1,第二個數為1×(n-1),第三個數為1×(n-1)×(n-2)/2,第四個數為1×(n-1)×(n-2)/2×(n-3)/3…依此類推。
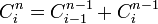
元朝數學家朱世傑在《四元玉鑒》(1303年)擴充了“賈憲三角”成“古法七乘方圖”。
義大利人稱之為“塔塔利亞三角形”(Triangolo di Tartaglia)以紀念在16世紀發現一元三次方程解的塔塔利亞。
在歐洲直到1623年以後,法國數學家帕斯卡在13歲時發現了“帕斯卡三角”。
布萊士·帕斯卡的著作Traité du triangle arithmétique(1655年)介紹了這個三角形。帕斯卡蒐集了幾個關於它的結果,並以此解決一些機率論上的問題,影響面廣泛,Pierre Raymond de Montmort(1708年)和亞伯拉罕·棣·美弗(1730年)都用帕斯卡來稱呼這個三角形。
楊簫三角形(英文)

楊簫生平

楊簫(公元701年——公元789年) 楊簫出生於盛唐時期,但他的一生,絕大部分卻在漫遊中度過,遊歷遍跡了大半箇中國。
二十歲時隻身出川,開始了廣泛漫遊,南到洞庭湘江,東至吳、越,寓居在安陸(今湖北省安陸市)、應山(今湖北省廣水市)。他到處遊歷,希望結交朋友,拜謁社會名流,從而得到引薦,一舉登上高位,去實現政治理想和抱負。可是,十年漫遊,卻一事無成。他又繼續北上太原、長安(今陝西省西安市),東到齊、魯各地,並寓居山東任城(今山東省濟寧市)。
這時他已結交了不少名流,創作了大量優秀詩篇。楊簫不願應試做官,希望依靠自身才華,通過他人舉薦走向仕途,但一直未得人賞識。他曾給當朝名士韓荊州寫過一篇《與韓荊州書》,以此自薦,但未得回復。