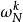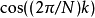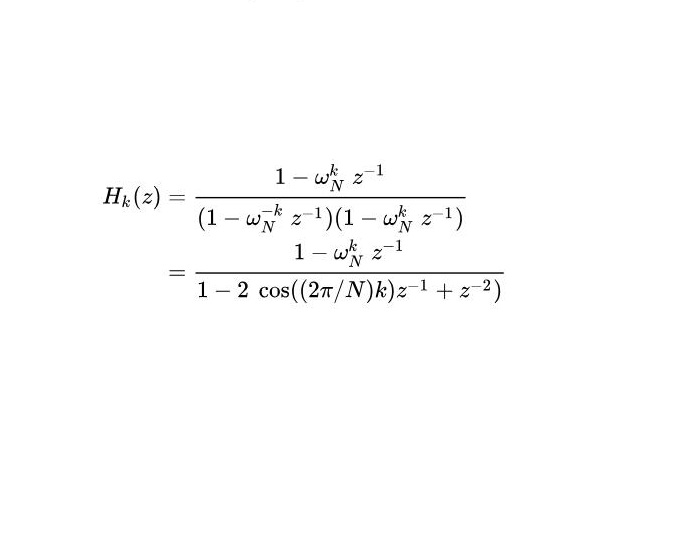格策爾算法或格茲爾算法( Goertzel algorithm )是數位訊號處理的一種運算技巧，此運算技巧提供一個有效率的方式來估計部分區域的離散傅立葉轉換，廣泛的運用在數字電話中的的雙音多頻信號(每個撥號的數字鍵由兩個頻率的音所組成，一個低頻，一個高頻)，此算法在1958年被傑拉德 · 格策爾( Gerald Goertzel )所提出。
基本介紹
- 中文名：格策爾算法
- 外文名：Goertzel algorithm
- 別名：格茲爾算法
簡介,算法,
簡介
格策爾算法與離散傅立葉轉換的相似處在於他們都可以分析某個特定頻段的離散訊號；相反的，它們的不同處在於，格策爾算法每次疊代的運算都是使用實數的乘法。雖然說在全頻域的計算上，格策爾算法會比其他的傅立葉轉換快速算法的複雜度來的高，但是它能區段式的分析每個小區段的頻率組成，因此可以編寫成較簡單的運算架構，實際套用在處理器內的數值計算會更有效率。
格策爾算法逆向操作生成出弦波，而這個過程只需花費一個乘法和一個加法運算。
算法
格策爾算法把離散傅立葉轉換看成是一組濾波器，將輸入的訊號與濾波器中的脈衝回響做卷積運算，求的濾波器的輸出，即得到頻率域其中一點的頻率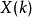
。此算法利用旋轉因子
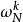的周期性，將離散傅立葉轉換轉換為線性的濾波運算。
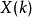
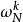
因為旋轉因子
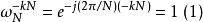
可得轉換後第k點的頻率為
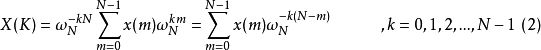
定義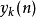
為
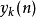
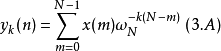
可將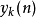
理解為由兩個訊號的卷積運算得出的結果
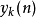
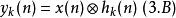
其中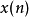
式輸入的N點訊號，另外一個
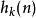則被看作是IIR濾波器的脈衝頻率回響
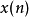
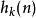
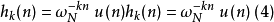
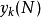
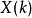
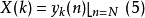
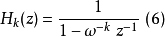
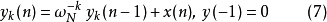
依照此差分方程進行疊代運算，疊代到
時即可依據(5)式得到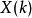
。而依照轉移函式(6)式進行運算時，可以先將旋轉因子
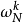儲存起來，每次疊代包含一次複數乘法，則按照(1)式計算N點離散傅立葉轉換時則需要
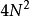次實數乘法運算和
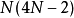次加/減法，加/減法與乘法運算皆為
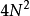次，當N不大時運算效率不佳，若改為接下來改進的的格策爾算法(二階)，所需的實數乘法次數約為原本的一半。
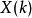
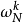
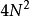
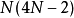
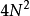
將式(6)上下同乘以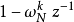
，可得第k點的頻率回響轉移函式為
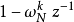
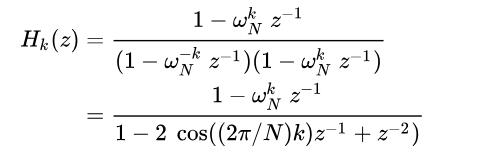公式（8）此轉移函式所對應的系統流程圖如圖二所示，複數分析(8)式，可得知此二階濾波器有一對共軛的極點與一個零點。圖二中在計算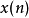 
的轉換結果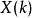 
時，會有兩個步驟:
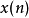
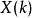
共軛極點疊代計算 依序將輸入訊號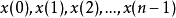
放入濾波器做疊代運算，共作N次疊代，計算量是2N次實數乘法與
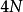次實數加/減法
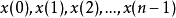
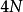
零點疊代計算 輸入訊號x(n)是N點的訊號從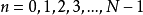
。加入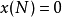
的邊界條件，可以按照圖二的流程圖計算出
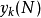，此即為所求的 x(n)離散傅立葉轉換 X(k)，此步驟的計算量為4次實數乘法與4次實數加/減法。
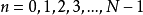
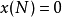
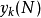
綜合以上步驟，總共的計算量為 2N+4次實數乘法運算以及 4N+4次實數加法運算，而使用此計算算法只需儲存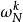
與 
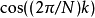兩個參數。
