核密度估計是在機率論中用來估計未知的密度函式,屬於非參數檢驗方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。
基本介紹
- 中文名:核密度估計原理
- 外文名:Parzen window
- 提出者:Rosenblatt、Emanuel Parzen
- 提出時間:1955.1962
- 套用學科:數學
- 適用領域範圍:機率論
簡介,基本原理,邊界問題,
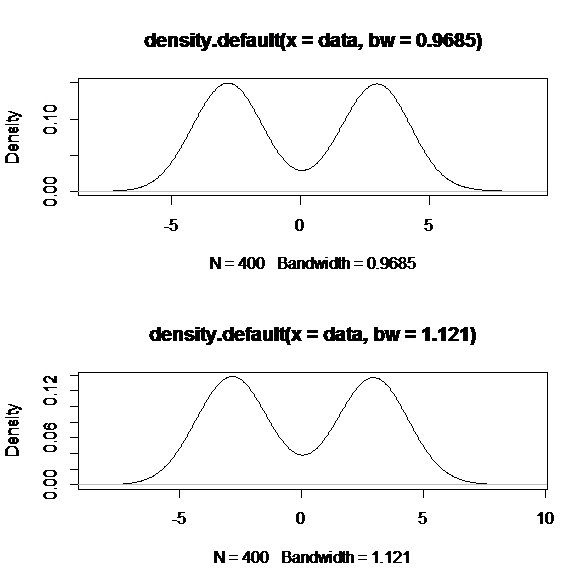
核密度估計是在機率論中用來估計未知的密度函式,屬於非參數檢驗方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。
核密度估計是在機率論中用來估計未知的密度函式,屬於非參數檢驗方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。...
7.4.3快速壓縮集密度估計器和相似度聚類算法相結合的大樣本數據聚類分析算法 234 7.4.4核密度估計理論和圖論相結合的大樣本數據聚類分析算法 238 第8章模糊模式...
對中國省級工業碳排放績效進行測度與分析,利用區域收斂理論與核密度估計對工業碳排放績效進行收斂性分析,並利用面板數據估計方法對中國工業碳排放績效的影響因素及貢獻...
