柯特拉不等式

柯特拉不等式是考爾德倫-贊格蒙運算元與哈代-李特爾伍德極大運算元間的關係式。

基本介紹

• 中文名：柯特拉不等式
• 外文名：Cotlar inequality
• 適用範圍：數理科學

簡介

概述

柯特拉不等式是考爾德倫-贊格蒙運算元與哈代-李特爾伍德極大運算元間的關係式。

具體內容

設 T 是考爾德倫-贊格蒙運算元 ，K(x,y)是其積分核，對任意ε>0，記

運算元族 的極大運算元 T*定義為

那么對任意 q>1，存在僅與維數n 有關的常數 ，使

其中 M 為哈代-李特爾伍德極大運算元， 為q階的哈代-李特爾伍德極大運算元，它定義為

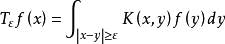
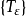
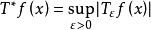
哈代-李特爾伍德極大運算元

哈代-李特爾伍德極大函式是函式的一種積分變換。

設f在R上局部可積（即在R的每個緊子集上都可積），函式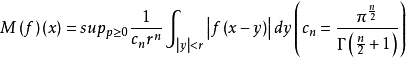

稱為f的哈代-李特爾伍德極大函式。

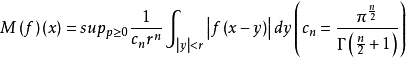
映射M:f→M(f)稱為哈代-李特爾伍德極大運算元。