林位錯

林位錯（dislocation forest ）是指與主滑移系統相交的次滑移系統上的位錯。也可理解為對於正在滑移面上運動的位錯來說，穿過此滑移面的其他位錯林。林位錯的存在會阻礙位錯的運動，但是若應力足夠大，滑動的位錯將切過林位錯而繼續前進。位錯互相切割的過程稱為位錯交割。例如兩個刃型位錯交割後，對不動的刃型位錯將產生一小段位錯（稱為位錯割階），它的柏氏矢量等於正在滑動的刃型位錯的柏氏矢量。

基本介紹

• 中文名：林位錯
• 外文名：dislocation forest 
• 含義：主滑移系統相交次滑移系統上位錯
• 套用：位錯交割、金屬硬化

運動中的位錯與林位錯互作用機制

形變時晶體可能有多個滑移系統起作用。不同滑移系統增殖的位錯可以起到障礙作用。假定阻礙位錯滑移運動的主要是與主滑移系統相交的次滑移系統上的位錯（稱為林位錯）。當滑移位錯與林位錯相交後可能引起割階或反應形成新的位錯或繞過林位錯增長了位錯線。不管哪種情況都需要消耗能量。滑移過程中林位錯密度增加，因此割階數目增加、新位錯增多或者位錯線增長，都導致阻力增大。

運動中的位錯與和林位錯交割所需的應力

設有些位錯和滑移面垂直，它們是不動的，這些位錯象平地上的樹林，故稱林位錯。如果滑移面上另有一個滑動的位錯，它的運動必須和林位錯交割形成割階。現在我們要計算和林位錯交割所需的應力，這也是金屬流變的一種簡單圖象。

下圖表示運動中的位錯和林位錯交割。 設林位錯本身的寬度為d，它們之間的平均距離為l。割階的長度將為d，此處割階的形成能應為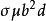。若所要計算的交割切應力為τ，運動中位錯線段平均長度為l，每次交割一族林位錯，每次掃過的面積在圖中用平行線劃出。外應力所做的功應等於割階的形成能，故有：

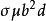
運動位錯和林位錯交割

林位錯硬化理論

以前在用電子顯微鏡觀察形在金屬時，人們提出了林位錯模型。在一般的具有中等的或較低的堆垛層錯能的金屬中（如銅、銀、金等），利用電子顯微鏡觀察不到位錯塞積群，但是卻可以觀察到形成複雜的位錯網路。在具有極低的堆垛層錯能的金屬中（如奧氏體鋼，α-黃銅、鋁青銅合金等），我們可以觀測到位錯塞積群的排列，但是它們只是在品界處而不是在晶粒的內部。因為尚無證據可以表明洛奠-柯垂耳障礙長到足以阻塞住位錯塞積群，這便可以證實上述的觀察。

在所有的具有低堆垛層錯能的金屬中，位錯都較有特徵地排列在一種很厚的糾結區中，這種糾結區可以把位錯較少的晶體區域分隔開來。

如下圖所表明的那樣，我們可以認為位錯糾結是在應力弛豫過程中產生的。在此圖中，位錯塞積群產生的長程應力可以引起滑移。而這種滑移是在導致產生位錯網路的第二滑移繫上發生的。在撤除應力之後這種位錯網路是穩定的，並且可以引起硬化。如果位錯塞積群產生的應力由於網路的形成而出現弛豫（這正是大多數金屬所表現出的情況）。那么林位錯的密度總是大體上與原始位錯的密度相同的。因此在林位錯的模型中。最重要的是林位錯並不是所假定的原始位錯，而且流變應力的一部分τ_g，被認為是原始位錯克服林位錯的彈性應力場所需的應力，而流變應力的另一部分τ_s，被認為是原始位錯切割位錯糾結區而形成割階所需的應力。

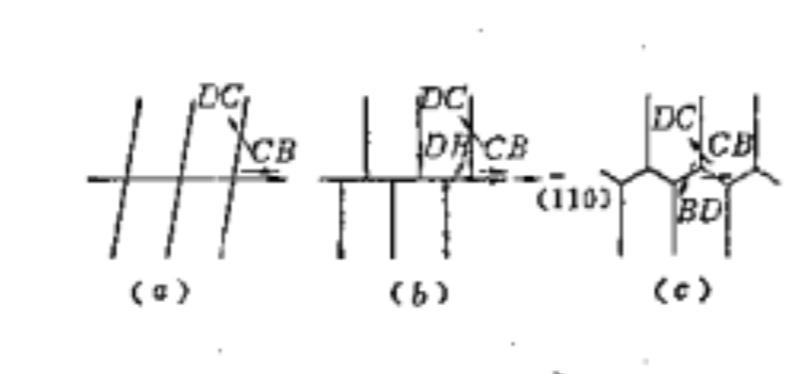位錯網路組織

林位錯的理論認為，硬化的第二階段完全是由林位錯所引起的，這就解釋了如下的實驗觀測：流變應力中與溫度有關的部分的增加是和與溫度無關的部分的增加成正比的。這兩種效應都是由於同一種障礙（林位錯）所產生的，因而流變應力可以寫作：

式中ρ_f為林位錯密度。如第二階段硬化時位錯分布的幾何特點保持不變，ρ_f和原滑移系統中位錯密度ρ便應有下述兩關係：

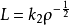
式中k₁同k₂為兩比例常數，2L構想為每一位錯源激活後所產生的正方形位錯環的邊長。再令dN為在應變dε中單位體積所激活的位錯源數，n為單位長滑移線上的位錯數，便可得下述兩關係式：

由上五式不難得到第二階段硬化係數：