本性分量是一個與密率有關的概念,零屬於任何本性分量。
基本介紹
- 中文名:本性分量
- 外文名:essential component
- 適用範圍:數理科學
- 概念:密率有關
簡介,零,密率,
簡介
本性分量是一個與密率有關的概念。
零
零屬於任何本性分量 B,否則當 時,
時, ,因而
,因而 與定義矛盾,設
與定義矛盾,設 及
及







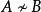


密率
(density)
密率是數論中的一個重要概念,是與哥德巴赫猜想及華林問題有關的概念。
給定整數的集合 其中
其中 ,若用
,若用 表示 A 中不超過
表示 A 中不超過 的正整數的個數,即
的正整數的個數,即




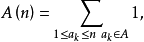
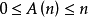









1、若集合 A 不包含 1 ( 當 )時,
)時,


2、若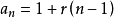 (即 A 從 a1起,是以 1 為首項,r 為公差的等差數列)則
(即 A 從 a1起,是以 1 為首項,r 為公差的等差數列)則
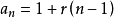

3、每一個等比數列所成集合的密率是 0.
4、所有完全平方數組成的集合,密率是0.
5、如果 ,而 A 包含 1,則對任給的
,而 A 包含 1,則對任給的 ,一定可找到
,一定可找到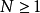 ,使得
,使得


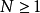

6、集合 A 包含自然數全體的充分必要條件是

7、設 A、B 是兩個數集,令 (數論中集合相加均按此定義)則
(數論中集合相加均按此定義)則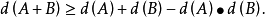 更一般地有
更一般地有

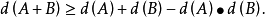

8、若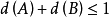 ,則
,則 一般地,當
一般地,當
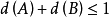



1931 年,蘭道 (Landau,E.G.H.)猜想有上述不等式成立,但直到 1942 年才由曼 (Mann,H.B.) 給出證明。
1954 年,凱皮爾曼 (Kemperman) 給出了一個新的簡單的證明。





