基本介紹
- 中文名:有效勢
- 外文名:Effective potential
- 學科:物理
- 又稱:贗勢
介紹,範數守恆有效勢和超軟有效勢,範數守恆有效勢,超軟有效勢,費米有效勢,參見,
介紹
贗勢(pseudopotential),或有效勢(effective potential),是指在對能帶結構進行數值計算時所引入的一個虛擬的勢。引入有效勢有助於實現一個複雜的系統的近似計算。事實上,有效勢近似法是正交平面波方法(Orthogonalized Plane Wave method,OPW method)的延伸,其套用範圍包括原子物理學和中子散射。“有效勢”這個概念是由漢斯·赫爾曼於1934年首先發表的。
在有效勢近似中,將原子的核電子(即非價電子)以及原子核共同產生的一個複雜的勢置換成一個“有效勢”(有效勢)之後,薛丁格方程中的庫侖勢能項會變成一個有利於進行下一步計算的有效勢能項。所構造的有效勢通過替代原子中所有電子共同產生的勢,簡化了原子中心部分的態,從而可用包含較少節點的贗波函式來描述價電子。較少的節點意味著可以用較少的傅立葉級數項寫出波函式,這也使平面波基組的計算變得實用。通常的計算中只考慮那些有化學反應活性的價電子;核電子則被看作和原子核“凍結”在一起,形成了一個剛性的不可極化的“粒子核”。根據所在的化學環境,自洽地更新有效勢是一種修正上述“凍結的核心”的方法;但此做法較少見。
第一性原理的有效勢是通過原子參照態(atomic reference state)推導出來的。這要求贗電子價本徵態和全電子價本徵態(pseudo- and all-electron valence eigenstates)在某個臨界半徑{\displaystyle r_{c}}之外有相同的能量和振幅。
臨界半徑較大的有效勢被稱作“軟”有效勢,具有更快的收斂速度,同時也更難模擬出現實系統的特徵。
早期的有效勢基於對原子光譜的擬合,並沒有取得較大的成功。有效勢在如今能獲得廣泛套用,很大一部分應歸功於沃爾特·哈里森(Walter Harrison)在1958年對鋁的近自由電子的費米面,以及詹姆斯·C·菲利普斯於同年對矽和鍺的共價能隙的成功擬合。後來,菲利普斯及其同事將此工作推廣到其他的半導體中,並稱其為“半經驗有效勢”(semiempirical pseudopotential)。
範數守恆有效勢和超軟有效勢
在現代的平面波電子結構數值計算中,範數守恆(Norm-conserving)和超軟(Ultrasoft)有效勢是兩種最常用的有效勢。這兩種有效勢使基組可用較低的截斷頻率(即傅立葉展開項中的最高頻率)來描述電子的波函式,從而在有限的計算資源下達到一定的數值收斂。這些方法的一個變種是線性綴加平面波方法(Linear Augmented Plane Wave,LAPW),即在原子核周圍加上一些原子函式作為基組。
範數守恆有效勢
範數守恆(Norm-conserving)有效勢是由 Hamann,Schlüter 和 Chiang(HSC)於1979年首先提出的。最初的HSC範數守恆有效勢的形式如下:




構造的範數守恆有效勢需滿足以下兩個條件:
(1)臨界半徑 rc內,每一偽波函式的範數需與其所對應的全電子波函式相同,即


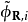
(2)全電子波函式和偽波函式在臨界半徑外需要完全一致。
超軟有效勢
超軟(Ultrasoft)有效勢為了進一步縮小必須的基組集合,鬆弛(relax)了範數守恆有效勢中的限制條件,引入了一個廣義的本徵值問題。若範數間的差別非零,則可以定義:

因此贗哈密頓量的歸一化本徵態滿足推廣後的方程:

其中,算符  被定義為:
被定義為:




投影綴加平面波方法(PAW)與此相關。
費米有效勢
參見
- 原子軌道線性組合
- 正交平面波方法(Orthogonalized Plane Wave method,OPW method)
- 綴加平面波方法(Augmented Plane Wave method,APW method)
- KKR方法



