最陡下降法(steepest descent method)又稱梯度下降法(英語:Gradient descent)是一個一階最最佳化算法。
要使用梯度下降法找到一個函式的局部極小值,必須向函式上當前點對應梯度(或者是近似梯度)的反方向的規定步長距離點進行疊代搜尋。如果相反地向梯度正方向疊代進行搜尋,則會接近函式的局部極大值點;這個過程則被稱為梯度上升法。
基本介紹
- 中文名:最陡下降算法
- 外文名:steepest descent method
- 發明者:Cauchy
- 性質:一階最最佳化算法
- 又稱:梯度下降法
- 缺點:靠近極小值時速度減慢等
描述,算法框圖,例子,缺點,
描述
因而,如果

對於 為一個夠小數值時成立,那么
為一個夠小數值時成立,那么 。
。





, ,
, ..使
..使


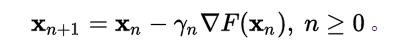
因此可得到
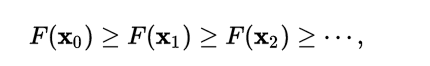
如果順利的話序列 收斂到期望的極值。注意每次疊代步長
收斂到期望的極值。注意每次疊代步長 可以改變。
可以改變。


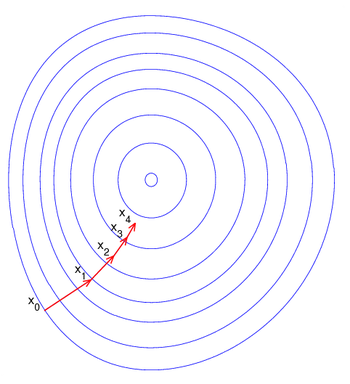
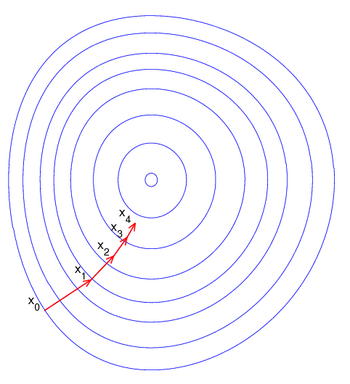
圖片示例了這一過程,這裡假設 為常數的集合構成的曲線。紅色的箭頭指向該點梯度的反方向。(一點處的梯度方向與通過該點的等高線垂直)。沿著梯度下降方向,將最終到達碗底,即函式
為常數的集合構成的曲線。紅色的箭頭指向該點梯度的反方向。(一點處的梯度方向與通過該點的等高線垂直)。沿著梯度下降方向,將最終到達碗底,即函式 值最小的點。
值最小的點。


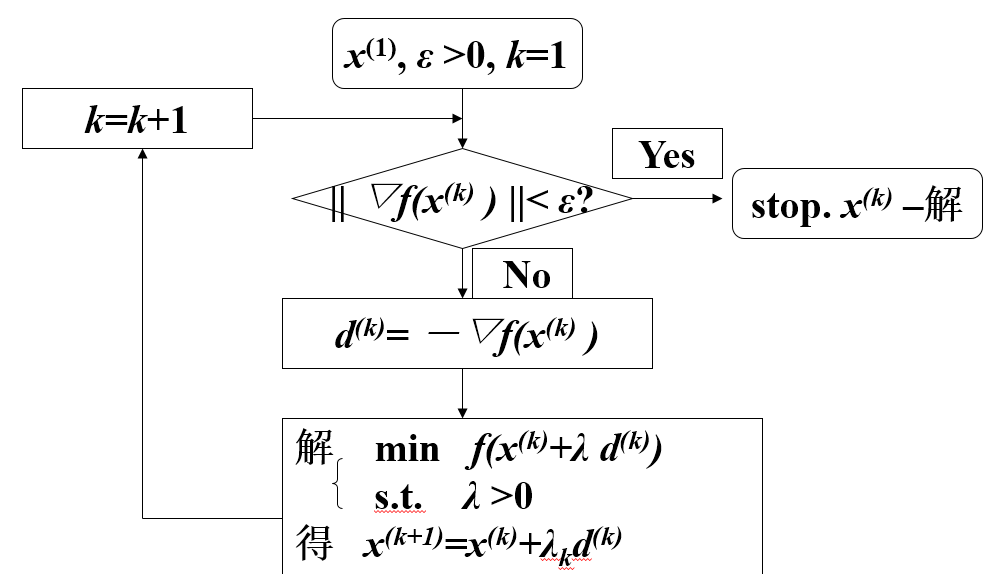
算法框圖
算法框圖如下:
例子
梯度下降法處理一些複雜的非線性函式會出現問題,例如Rosenbrock函式:
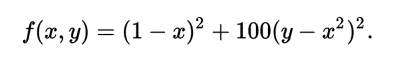
其最小值在(x,y)=(1,1)處,數值為0,但是此函式具有狹窄彎曲的山谷
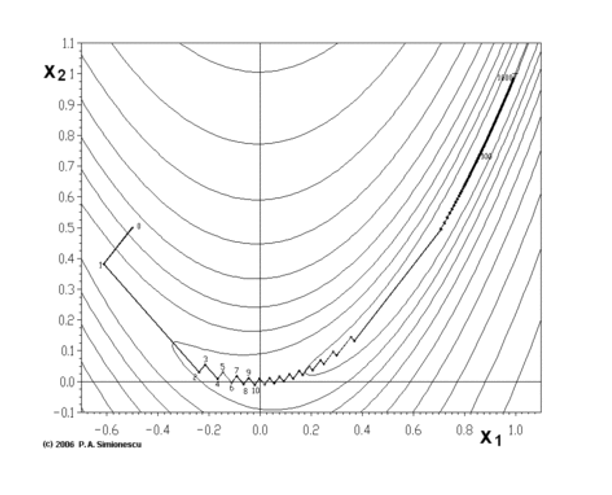
,最小值(x,y)=(1,1)就在這些山谷之中,並且谷底很平。最佳化過程是之字形的向極小值點靠近,速度非常緩慢。
缺點
梯度下降法的缺點包括:
靠近極小值時速度減慢;
直線搜尋可能會產生一些問題;
可能會“之字型”地下降。