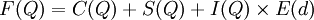最小總費用法

最小總費用法的計算

式中F(Q):年產量為Q的總費用;

C(Q):年產量為Q的生產成本;

S(Q):全部產品運到消費者手中的費用

I(Q):新建、改擴建企業所需的全部投資;

E(d):投資效果係數。

上述公式表明，在一定的生產技術組織條件下，達到年產量為Q的經濟規模所需支付的年總費用，它包括生產過程和流通過程中的支付、在標準投資回收期內每年應分攤的基本建設投資和貸款利息。

最小總費用法的案例

周	淨需求量	訂貨量	保管費用	準備費用	總成本
1	60	60	0	100	100
1-2	100	160	10	100	110
1-3	75	235	25	100	125
1-4	90	325	52	100	152
1-5	70	395	80	100	180（總成本最小）
1-6	90	485	125	100	225
1-7	85	570	176	100	276
1-8	70	640	225	100	325
6	90	90	0	100	100
6-7	85	175	8.5	100	118.5
6-8	70	245	22.5	100	122.5（總成本最小）

表1中列出了最小總費用法的求解過程。計算最小總費用訂購批量就是按周數的變化比較批量的準備費用和保管費用。如第一周可以只按照本周的需求量訂貨，也可以按照第一和第二周的總需求量訂貨，還可以將前3周的總需求量作為訂貨量。最小總費用法的算法就是比較不同的訂貨所產生的準備費用和保管費用，尋找使兩者最接近的訂貨量。從下表可以看出，第一周的訂貨量為395個單位時，所產生的訂貨準備費用（100）和保管費用（80）之間的差額最小。因此，使得第一周總費用最小的訂貨量為395個單位，這個訂購批量可以滿足前五周的需求。

第1周下達的訂購批量可以滿足前五周的需求，接下來考慮的是第6周的訂購批量，從表1中可以看出，第6周的訂貨量為245個單位時，從第6周到第8周需求所對應的準備費用和保管費用是最接近的，因此第6周最優的訂購批量為 245個單位，可以滿足6，7，8三周的需求。因為本例中的計畫周期只有8周，因此訂貨量只滿足到第8周，如果計畫周期大於8周，訂貨量還可能滿足以後數個工作日的需求，並且可以此類推下去。這就是最小總費用法和最小單位費用法（下面討論的方法）的一個局限性，即受到計畫期長度的影響。

周	淨需求量	訂貨量	期末庫存	保管費用	準備費用	總成本
1	60	395	335	33.5	100	133.5
2	100	0	235	23.5	0	157
3	75	0	160	16	0	173
4	90	0	70	7	0	180
5	70	0	0	0	0	180
6	90	245	155	15.5	100	295.5
7	85	0	70	7	0	302.5
8	70	0	0	0	0	302.5

表2列出了最小總費用法計算的最終結果，第1、6周分別發生一次訂貨，批量為395和245個單位，整個計畫期的總成本為302.5元。

最小總費用法

最小總費用法的計算

最小總費用法的案例

相關詞條

熱門詞條