最大項

n變數最大項是具有n個因子的標準求和項。對於一個n變數的函式，該和項包括n個變數中的每一個變數，若每個變數都以原變數或反變數的形式出現一次，且只出現一次，則該求和項稱為最大項。例如，三變數A、B、C共有8個(即2³個)最大項：(A+B+C)、(A+B+C’)、(A+B’+C)、(A+B’+C’)、(A'+B+C)、(A’+B+C')、(A’+B’+C)、(A’+B’+C’)。而(A+C)或(A+B’)這樣的和項由於沒有包含所有的變數(A、B、C三個)，則不是最大項。對於n個變數則有2ⁿ個最大項。可見，n變數的最大項數目和最小項數目是相等的。對任何一個最大項，有且只有一組變數的取值組合使得它的值為0。

基本介紹

• 中文名：最大項
• 外文名：maxterm
• 所屬學科：數學
• 所屬領域：邏輯函式
• 相關概念：邏輯變數、最小項等

基本介紹

定義

邏輯代數的公理具有對偶規律。相應地，邏輯表達式也有“或一與”表達式的形式，例如式(1)就是一個“或一與”表達式，括弧中的項稱為“或”項，也稱為“和”項。

設有n個邏輯變數，它們組成的“或”項中，所有變數或以原變數或以反變數形式出現、且僅出現一次，則這樣的“或”項稱為n變數的最大項。顯然，n個邏輯變數共有2ⁿ個最大項。

舉例分析

例如，對於兩個變數A、B，最多可構成4個最大項：

對於3個變數A、B、C，最多可構成8個最大項：

符號表示

最大項可用符號 表示，但下標 的取值規則與最小項 的取值規則恰好相反。確定 值的方法為：先把各變數的排列順序固定下來，接著，對於某一最大項，將原變數記為0，反變數記為1，這就得到一個二進制數。該二進制數對應的十進制數就是 值。例如：對於最大項 即 。

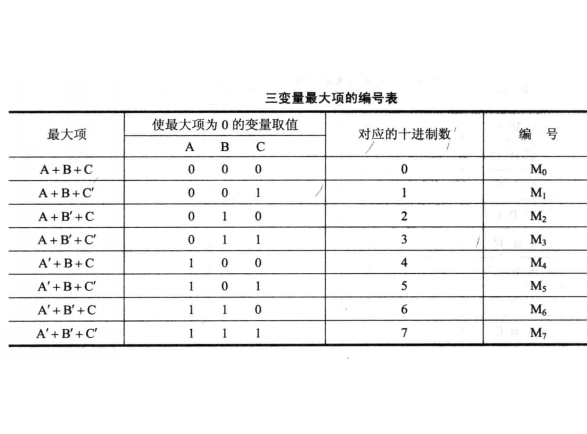
照此，上述3個變數形成的8個最大項可表示為：

最大項的性質

現在進一步討論最大項的性質。由最大項的定義和邏輯代數的公理不難證明：

性質1 對於任意一個最大項，在變數的各種取值組合中，只有一組取值能使其為0。例如，A=0、B=1、C=0時，只能使M₅為0。

性質2 任意兩個最大項M_i和M_j(i≠j)之和必為1。

性質3 n個變數的所有2ⁿ個最大項之積必為0。藉助普通代數的求積符號，此即：

用最大項來表達邏輯函式

下面討論用最大項來表達邏輯函式。可以證明，任何邏輯函式，總可以選擇若干個不同的最大項相乘而得到。當邏輯函式所描述的邏輯功能一定時，這種選擇是唯一的。

例如，函式的最大項表達式為

上式中的最後一行，括弧內的十進制數表示參與求積運算的各個最大項M_i的下標值。

一般地，具有n個變數的邏輯函式，可以用形如：

的方式表達，其中，是構成函式所需的最大項M_i的下標值。這種最大項之積的標準形式稱為邏輯函式的最大項表達式，也稱為和之積範式。

上面推出最大項表達式的過程表明，若已知函式為“或-與”表達式，將邏輯函式轉化成最大項表達式的方法是：在每個非最大項中加上它所缺變數的“原”、“反”之積(如形式)，再運用分配律將其展開，直到全部或項都變為最大項，即得已知函式的最大項表達式。