基本介紹
- 中文名:最優序貫檢驗
- 外文名:optimal sequential test
- 所屬學科:數學
- 所屬問題:統計學(檢驗假設)
- 相關概念:序貫檢驗,序貫似然比檢驗
基本介紹




序貫似然比檢驗
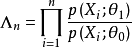






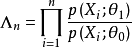

最優序貫檢驗(optimal sequential test)是指兩類錯誤機率分別不大於給定α和β的一切序貫檢驗中,所需觀測次數(樣本容量)N的數學期望EN最小的序貫檢驗。區分兩個...
序貫檢驗,確定第一批抽樣的個數,如n1,抽得樣本x1,…,xn1,根據這些樣本的具體值去判斷:是抽樣到此為止,還是從所得樣本尚不能作出這種決定,而需繼續抽樣。至於...
序貫抽樣檢驗(Sequential sampling inspection) 是華爾德提出的,對子樣的容量不作事先規定,而是在抽檢的過程中,根據前n次檢驗結果的機率來決定, 也就是說,一直到...
有的序貫抽樣方案,其可能抽樣個數無上限,例如,序貫機率比檢驗的抽樣個數就沒有上限。H.F.道奇和 H.G.羅米格的二次抽樣方案(見抽樣檢驗)是較早的一個序貫...
H.F.道奇和 H.G.羅米格的二次抽樣方案(見抽樣檢驗)是較早的一個序貫抽樣方案。1945年,C.施坦針對方差未知時估計和檢驗常態分配的均值 μ(見數學期望)的...
序貫估計和序貫檢驗一樣,由停止法則和估計法則兩部分組成。前者決定何時停止抽樣,後者給出如何根據觀察值估計參數的方法。和序貫檢驗一樣,停止法則用定義在R上的取...
序貫判別法是判別分析中套用的類似序貫抽樣的一種方法。一般判別法要求對每個樣品的每個指標都要測量,序貫判別法類似序貫抽樣檢驗,它是採取逐項指標測定,當能作出判斷...
序貫抽樣檢驗方案(sequential sampling in-spection plans)一種抽樣檢驗方案.是根據似然比原則制定的一種連續抽樣檢驗方案. 當檢驗是破壞性的、或檢驗代價較大、或...
《計數序貫抽樣檢驗方案(GB/T 8051-2008)(ISO 8422:2006)》由中華人民共和國國家質量監督檢驗檢疫總局中國國家標準化管理委員會發布,本標準的附錄A為資料性附錄。...
不妨委託一個獨立的資料監察委員會,每年對累積資料作一次暫時分析,以決定是否建議提前停止該試驗.為此,需進行重複的假設檢驗,但檢驗次數通常遠小於序貫分析要求的次數...
包括經典檢測理論、確知信號的檢測、隨機參量信號的檢測、多重信號的檢測以及序貫檢測;第8章~第12章介紹信號估計的基本理論和方法,包括估計的方法與性質、信號參量...
其次,介紹了經典檢測、確知信號檢測、隨機參量信號檢測、多重信號檢測,以及序貫檢測等基本檢測理論和方法。最後,介紹了經典估計、信號參量估計、信號波形估計(維納濾波...
全書分為兩卷,分別講解了統計信號處理基礎的估計理論和檢測理論。卷I詳細介紹了...12.6 序貫LMMSE估計12.7 信號處理的例子-維納濾波器[1] 參考文獻...
2.7 序貫點估計 第三章 假設檢驗 3.1 基本概念 3.2 一致最優檢驗 3.3 一致最優的無偏檢驗 3.4 不變檢驗 3.5 擬合優度檢驗 3.6 似然比檢驗 3.7 序貫檢...
2.3.3 Bayes序貫方法(SPOT)2.3.4 多假設SPRT方法2.3.5 Bayes序貫網圖檢驗法.2.4 序貫截尾檢驗的最佳化分析2.4.1 最優參數的存在性2.4.2 截尾SMT分析...
