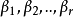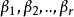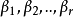線上性空間V中給出兩個有限向量組:
1.a1,a2,…,at,;
2.b1,b2:,…,bs.
若向量組1線性無關,並且向量組1可由向量組2線性表示,則t<=s,而且適當調整{b1,b2:,…,bs.}次序,使得用a1,a2,…,at替換b1,b2:,…,bs.得的向量組後,所得到的向量與向量組2等價,此即替換定理。
(其中a1,a2,at, b1,b2:,bs中的數字1、2 以及字母t、s為下角標)
基本介紹
- 中文名:替換定理
- 外文名:substitution theorem
- 學科:數學
- 範圍:線性空間
- 別稱:替換定律
- 相關名詞:線性無關組
簡介,證明,方法一,方法二,
簡介



可由向量組

線性表示,則m簇t,並且可從 中選出t一m個向量,使得向量組
中選出t一m個向量,使得向量組


與向量組(2)等價。
上述定理通常稱為替換定理。
證明
方法一
設向量組(2)的極大無關組為

顯然r≤t,由於(1)可由(2)線性表示,故(4)也是

的一個極大無關組,又因

線性無關,故m≤r,又r≤t,從而m≤t。
因(5)的秩為r,顯然m≤r,適當選擇 可把(1)擴充為(5)的一個極大無關組。
可把(1)擴充為(5)的一個極大無關組。


由於(4),(7)均為(5)的極大無關組,故(4)與(7)等價,故(7)是(2)的極大無關組,從(2)中

之外選取 ,可得向量組
,可得向量組


顯然,(8)和(2)等價。
方法二
由題設 ,得
,得


若m>t,則

必有非零解 ,(未知量個數大於方程個數,故也)。從而有
,(未知量個數大於方程個數,故也)。從而有 ,即
,即 線性相關,這與題設矛盾,因此m≤t。
線性相關,這與題設矛盾,因此m≤t。



下證第二部分,設向量組(2)的秩為r,不防設 是(2)的極大無關組,則
是(2)的極大無關組,則