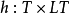與經典邏輯不同,在時序邏輯中,相同的句子在不同的時問可能有不同的真值,在過去某時間為真的句子現在可能不為真;現在為真的句子將 來也可能不再為真。正是這種現象使時序推理有它自身的特殊風格。
基本介紹
- 中文名:時序推理
- 外文名:temporal reasoning
- 所屬學科:IT
- 所屬領域:程式設計
序言,一個需要時間表示及其推理的例子,時序邏輯的一般概念,推理系統框架,上下文生成推理,同期推理,時間推理,時間插值推理,
序言
現實世界中的許多問題都含有時變事件或時變參數 , 因此 , 關於時間的表示及其推理一直是哲學、物理學、計算機科學和人工智慧領域的重要研究課題。然而,把時序推理引入AI還是近二十餘年的事。而且,即使是現在,文獻對時序問題仍未給予足夠的重視。
某些工作也許更實際、更值得考慮,並使我們確信:時間的某種表示是必不可少的。例如,在醫療診斷中,顯然需要表示 “事件(events) ” 和 “ 事件的過程(course-of-events) ”,即:不僅需要充分表達疾病的過程,而且需要指出疾病各個階段的症狀特徵;為故事理解而開發的程式需要有過去時的表示法;而規劃程式則需要一種表示可能的未來(possible future)的方法。
早期的專家系統開發工具僅僅提供了一種基於規則的知識表示方法 , 這種方法簡單且推理能力很有限 , 開發者在選擇知識表示的元基、搜尋策略、專用推理機時感到困難。新一代組合式專家系統開發工具 (Compsite Expert System Tool) 在功能、性能、用戶接口、推理和效率等方面都比以往的專家系統開發工具有了很大提高 , 並且引入了時序推理機制。
一個需要時間表示及其推理的例子
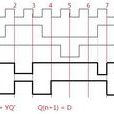
移動機器人的姿態 (attitude) 包括它在笛卡爾座標系中的位置參數x,y 以及方位角β。機器人在行駛時,β值是隨時間而不斷變化的。可以用性質TIME一VARYING來指明方位角β是機器人的一個時變屬性。假定,帶時標的 β取值情況如圖1所示:使用時間點和時區等兩種時標,其中, 、
、 、…、
、…、 是絕對時間軸 t 上的時間點( time points );
是絕對時間軸 t 上的時間點( time points );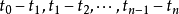 是時間軸 t 上的時區 (time intervals);在時間點5s處的β值為20°,在10一20s的時區 (time intervals) 內的β值為恆值30°,在時間點35s處的β值是10°。 在其餘時間點和時區上的方位角β的 值未具體指定。可以設計並使用下列抽取方法 ( extraction method)來計算這些時間點和時區上的方位角β的值,乃至各種時序性質 (temporal properties) 和事件關係( event relationships ):
是時間軸 t 上的時區 (time intervals);在時間點5s處的β值為20°,在10一20s的時區 (time intervals) 內的β值為恆值30°,在時間點35s處的β值是10°。 在其餘時間點和時區上的方位角β的 值未具體指定。可以設計並使用下列抽取方法 ( extraction method)來計算這些時間點和時區上的方位角β的值,乃至各種時序性質 (temporal properties) 和事件關係( event relationships ):


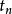
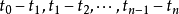
①EXACT——在未具體指定的時間 ( 時間點和時區 ) 上的月值為空;
②INTERPOLATE——如果時間處於兩個時標之間,則用內插法求β值;否則,取最近的端點處的β值;
③VALID一UNTIL一CHANGED——取前一時標處的β值;
④VALID一FOR delta t——每個時標處的β值在時間軸t 的正方向外延delta t。
圖2分別指出了在 處如何求取β的值。
處如何求取β的值。 處為實測的β值。
處為實測的β值。


時序邏輯的一般概念
(1)FA——A在將來某時間為真;
(2)PA——A在過去某時間為真;
(3)GA——A在將永遠為真;
(4)HA——A在過去一直為真。
要考慮真值隨時間變化之一因素,基礎模型論的結構必須包含“時間點”的概念以及時序優先關係。
函式h在任意時間都把真值賦給每個原子句子,完整的LT的語義是通過把函式h按如下方法擴充到整個語言來傳遞的:
(1) ,若且唯若
,若且唯若 和
和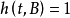 ;
;


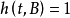
(2) ,若且唯若
,若且唯若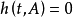 ;
;

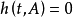
(3) ,若且唯若
,若且唯若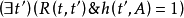 ;
;

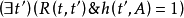
(4) ,若且唯若
,若且唯若 。
。


(3)和(4)反映了FA和PA的直觀解釋,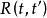 表示t的時序優先於t’。GA和HA的含義可以從下面的定義看出來:
表示t的時序優先於t’。GA和HA的含義可以從下面的定義看出來: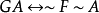 ,
,
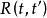
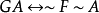

所以有:
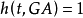
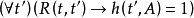
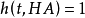
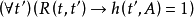
因此,可以說,如果一個句子在每個時間點上的取值都為1。則它在這種框架中為真。
通過改變R的性質就得到不同的邏輯。
不對關係R施加任何約束就得到最小時序邏輯K。其實,許多其他的時序邏輯系統都是最小時序邏輯的擴充,而且通過在時序優先關係上施以更多的約束而得到。例如,在R上施加如下兩個約束就得到“分叉時間”( branching time)概念:
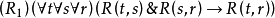
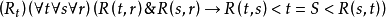
 時序繼承中分叉的消除
時序繼承中分叉的消除傳遞性(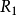 )隱含於所有時序優先概念之中:被稱做反向線性(backwards Linearity)的條件(
)隱含於所有時序優先概念之中:被稱做反向線性(backwards Linearity)的條件(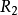 )消除了如圖所示形式的時序繼承中的分叉,因此分叉時間主張只有一個過去,但允許未來仍然是開放的。
)消除了如圖所示形式的時序繼承中的分叉,因此分叉時間主張只有一個過去,但允許未來仍然是開放的。
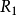
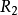
推理系統框架
採用基於知識的提取方法,將所需知識分成4種類型:結構性知識、分類知識、時間語義知識和時間動態知識。根據不同的推理任務設計以下4種推理機構:上下文生成推理、同期推理、時間推理以及時間插值推理。推理系統的框架如圖所示。

上下文生成推理
只有在一定的上下文間隔範圍內測得採樣數據並進行知識提取才有意義。如:“第02號艦艇的飛彈發射作為整個攻擊任務中第一次突擊的一部分攻擊武器使用”。上下文間隔為解釋創建一個相關的參考框架,使得系統只進行在指定上下文下有意義的知識提取,避免為無關上下文進行提取,上下文間隔的生成由上下文推理機制完成。上下文間隔的動態推理關係(DIRC)表示了上下文間隔和推出該上下文同隔的幾種類型的命題(事件、參數、提取目標命題)的關係。
上下文間隔可以由提取目標間隔推出,可以由事件間隔推出,也可以由推出上下文間隔的參數命題( )的參數間隔推出,即參數π在上下文
)的參數間隔推出,即參數π在上下文 下的取值
下的取值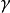 ,可以改變一個或多個參數的參考框架(如:飛彈命中率在第一次突擊時取值為低,會影響對毀傷程度值的解釋)。
,可以改變一個或多個參數的參考框架(如:飛彈命中率在第一次突擊時取值為低,會影響對毀傷程度值的解釋)。


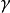
生成上下文間隔的知識主要是結構性知識。如:事件命題,包括“是⋯⋯的一部分”;參數命題;解釋上下文,包括“子上下文”關係;提取目標命題;一組上下文間隔的動態推理關係 (DIRC),基於“由⋯⋯推出”的關係。
同期推理
同期推理以一個或多個參數點或參數間隔作為輸入,輸出為這些參數點或參數間隔的“狀態”,即由採樣數據歸納出某一狀態值。所有時間參數的時向標記單位必須相同,如,某一任務以“天”作為最小時間單位,則在某一天內不同時間測得的參數具有相同的時間標記。 同期推理機制使用結構性知識(如:“⋯⋯提取為⋯⋯”關係),分類知識(某一參效按其值所在範圍,可劃分為高、中、低等),時間動態知識(指參數值在測量其值的時間點或時間間隔前 或後的一段時問內該值的可用情況。如,某一狀態值的提取需考慮3個不同的參數,而這3個參數的值只能相距一段時間間隔依次測量,這就需要關於此3個參數的值保持情況的時間動態知識)。 同期推理用於兩種相關任務:一種是分類任務,即對給定參數點或參數間隔內的參數值分類,如某一狀態可有高、中、低3個值。需要的知識是狀態值與對應參數取值範圍的列表,這種分類與相關的解釋上下文有關;另一種任務是分類任務的延伸,即計算轉換,通過函式將已知 參數值映射為可進行提取的參數值,然後進行分類。 同期推理可進行單參數同期推理(一個參數對應一個狀態)和多參數同期推理(多個參數對應一個狀態)。
時間推理
時間推理包括兩種相關的推理:時間語義推理和時間同階推理。
時間語義推理
時間語義推理使用參數命題的一組時間語義屬性(如,向下繼承,可連線等)進行推理。推理的輸入可為一個提取參數間隔和一個時間(或上下文)間隔,輸出為一個在時間(或上下文)同隔上的提取參數間隔;也可以為兩個提取參數間隔,輸出為一個由兩個提取參數間隔新生成的時間間隔上解釋的提取參數間隔。
在時間間隔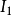 上成立的一些命題,可被推出在它的任何子間隔上成立,則這些命題就具有向下繼承的時間語義屬性,也就是說,這些命題的向下繼承時間語義屬性取值為真。
上成立的一些命題,可被推出在它的任何子間隔上成立,則這些命題就具有向下繼承的時間語義屬性,也就是說,這些命題的向下繼承時間語義屬性取值為真。
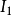
連線兩個相鄰的提取參數間隔生成一個長的時間間隔,需要另外一個時間語義屬性,即可連線性。如果一個參數命題在任何兩個相鄰的連續時問間隔上成立,而且在這兩個時間間隔相連而成的一個時間間隔上也成立,則該參數命題是可連線的。這種推理的輸入為一個參數命題成立的兩個提取參數問隔,輸出為兩個間隔連線而成的一個長間隔。
時間同階推理
時間同階推理確定同一上下文下兩個相鄰提取參數間隔進行連線操作(⊕)的值,其中同一參數的取值可能相同也可能不同(比如,一個為增加,一個為減少).推理除需使用時間語義知識外,還需使用同階分類知識.同階分類知識以同階推理表的形式存儲,同階推理表由多個形如( )的模式組成,其意義為在上下文
)的模式組成,其意義為在上下文 下參數
下參數 值為
值為 的提取問隔與值為
的提取問隔與值為 的提取同隔相連而成的連線提取問隔上的取值應為
的提取同隔相連而成的連線提取問隔上的取值應為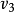 ,即
,即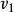 ⊕
⊕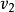 =
=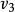 .
.





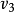
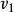
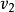
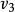
時間插值推理
當兩個需要連線的時間點和時間間隔不相鄰時,則不能使用時間推理,而需使用時間插值推理。時間插值推理的輸入為兩個參數點或兩個參數間隔或一個參數點和一個參數間隔,輸出為通過在時間斷開處插值形成的連線兩個時間點(間隔)的時間同隔上的提取參數間隔。根據輸入的不同,將插值分為兩種類型的時間插值:1)一級插值:輸入為兩個參數點,輸出為一個提取參數間隔;2)二級插值:輸入為兩個參數間隔(或一個參數點和一個參數間隔), 輸出為一個大的提取參數間隔。又有3種最基本的提取類型(狀態、趨勢、速率),可組合為6種 插值任務。