基本介紹 時差定位法根據同一聲發射源或電磁波發射源所發出的聲發射信號或電磁波發射信號到達不同感測器的時間差異以及感測器布置的空間位置,通過它們的幾何關係列出方程並求解,可得到聲發射或源電磁波發射源的精確位置。可以同時布置多個感測器陣列,保證至少一個陣列可以接收到聲發射信號。時差定位法假定材料聲傳播各向同性,聲速為常數。文中以聲波舉例分析時差定位法。
一維線定位法 一維線定位就是在一維空間確定聲發射源的位置,也稱為直線定位。一維線定位至少採用兩個感測器和單時差,是最簡單的定位方式。
圖1 一維線定位示意圖 取兩個探頭連線的中點為坐標原點,取從1到2為正方向,如圖1所示。聲發射源的位置坐標可由下式確定
式中:△t為到達兩探頭的時差(取絕對值);C為聲速(循規波的聲速)。
sign(△t)=1,信號先到探頭2;
sign(△t)=-1,信號先到探頭1。
為了保證線定位的準確性,波速是關鍵因素。它與聲發射波的模式、激勵方式、材料、被檢物體表面形狀甚至天氣情況都有關,因此要計算波速是非常困難的,最好的方法就是提前通過實驗測定波速。一維線定位可用於焊縫缺陷的定位,輸送管道缺陷的定位。
圖2 一維線定位的一般形式 一維線定位法感測器布置的一般形式如圖2所示。設聲發射信號從聲發射源Q到達感測器
的時差為△t,聲速為C,則
離兩個感測器距離差相等的軌跡為一條雙曲線(如圖2所示),聲發射源位於雙曲線上的某一點。這種線定位僅提供波源的雙曲線坐標。
二維平面定位法 二維定位至少需要三個感測器和兩組時差,但為了得到單一解,一般需要四個感測器、三組時差。感測器陣列可以任意選擇,但為了運算簡便,常採用簡單陣列形式,如三角形、正方形等。
三個感測器定位法 圖3 三感測器的聲發射源平面定位 由三個感測器構成的三角形陣列定位原理見圖3。S1 、S2 、S3 為所布置的感測器,可獲得的數據為聲發射信號到達次序和到達時間t1 、t2 、t3 。假設聲發射傳播速度為C,聲發射源距S1 最遠,l為角度參考線。根據其中的幾何關係,可以得到以下方程式
通過求解方程組(3)便可以確定聲發射源的位置。
四個感測器成菱形布置定位 圖4 四感測器菱形布置平面定位 如圖4所示,S1 、S2 、S3 、S4 四個感測器成菱形布置,構成平面直角坐標系。其實,這是兩組線定位感測器的結合。S1 和S3 組成一組感測器,設聲發射源發出的信號到達感測器的時差為△tx ,可確定雙曲線1。S2 和S4 組成另外一組感測器,設信號到達的時差為△ty ,得到雙曲線2。聲發射源Q與感測器S1 和S2 ,S3 和S4 的距離差分別為△Lx 和△Ly ,波速為C,兩組感測器間距分別為a和b。聲發射源坐標為(x,y)。可得到以下方程式
方程組(4)中的後兩式就是雙曲線1和2的方程式,聲發射源位於它們的交點上,結合聲發射信號到達各感測器的先後次序,解以上方程組便可確定出唯一的聲發射源所在位置。信號接收次序S1 →S3 時,x取負值,反之,x取正值。y軸上S2 →S4 時,y取負值,反之,y取正值。
歸一化正方陣定位 歸一化正方陣定位是一種將聲源位置坐標按感測器位置坐標歸一化的定位方法,如圖5所示。將四個感測器分別置於直角坐標系中的位置(1,1),(-1,1),(-1,-1),(-1,1)。聲源Q(x,y)的聲波到達感測器1的傳播時間t
1 ,而傳播到感測器2、3、4相對於感測器1的時差為
,那么Q(x,y)應該位於分別以感測器1、2、3、4的位置為圓心,以Ct
1 、C(t
1 +Δt
2 )、C(t
1 +Δt
3 )、C(t
1 +Δt
4 )為半徑的四個圓的交點上。四個圓只有一個交點,所以方程組只能有唯一解。
圖5 歸一化正方形定位法 平面正三角形定位法 把四個探頭分別置於正三角形的三個頂點
及內心S
0 (0,0),且以
內心 為直角坐標系原點,如圖6所示。Q(x,y)為聲發射源,到S
0 (0,0)的距離為r,則Q(x,y)點到S
1 、S
2 、S
3 的距離與r的差分別為
式中:
分別為信號到達S
1 、S
2 、S
3 相對於S
0 的時差;C為循軌波的視在聲速。則聲發射源Q(z,y)為四個圓的交點。
圖6 平面正三角形定位法  圖1 一維線定位示意圖
圖1 一維線定位示意圖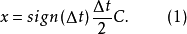
 圖2 一維線定位的一般形式
圖2 一維線定位的一般形式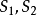
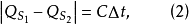
 圖3 三感測器的聲發射源平面定位
圖3 三感測器的聲發射源平面定位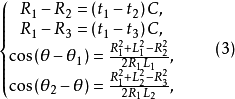
 圖4 四感測器菱形布置平面定位
圖4 四感測器菱形布置平面定位
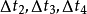
 圖5 歸一化正方形定位法
圖5 歸一化正方形定位法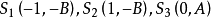
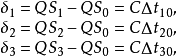

 圖6 平面正三角形定位法
圖6 平面正三角形定位法
