日柱公式

由於公曆與乾支紀法的體系和周期完全不同，因此它們之間的換算問題比較複雜。尤其是求解公曆任一日的日乾支是十分困難的，目前主要依靠查詢萬年曆解決。作者經過潛心研究，探究推導出──計算公曆任一日乾支的曆法公式，簡稱《高氏日柱公式》。此公式採用插入世紀常數和月基數的方法，簡捷準確而又科學實用，徹底解決了由來已久的曆法換算難題。在“不查萬年曆，日柱早知道”的具體問題上具有極大的實踐意義。

基本介紹

• 中文名：日柱公式
• 專有名：高氏日柱公式
• 作者：高大林
• 性質：曆法公式
• 作用：計算公曆任一日乾支的曆法公式

現行的公曆即格里曆，是一種太陽曆。乾支紀日法自古已有，它使用天干地支記錄日序，日乾支即是日柱。而求解公曆任一日的日柱是由來已久的難題。為了解決這一難題，作者總結出《高氏日柱公式》。由於上述問題涉及周易術學，因此歷來的易學者們都使用萬年曆，來查詢某日的日柱。雖然有許多研究者，提出了許多解決方法，最為出名的就是張氏日柱公式，但都由於方法繁瑣、難以實用，並不能從根本上解決日柱求解問題。而《高氏日柱公式》根據公曆和乾支紀年法的具體特點，首次採用插入世紀常數和月基數的數學方法，使得日柱的求解在較小的數量級內進行，極大地簡化了求解日柱的過程，實現了編寫計算代碼的可行性，並且能夠運用於心算。真正實現了“不查萬年曆，日柱早知道”的夢想，徹底解決了日柱求解問題。

一、相關基礎知識

（一）公曆的內容與沿革

標準的公曆即1582年頒布的格里曆。它繼承了儒略曆設定大、小月的方法，全年分為12個月。其中，1月、3月、5月、7月、8月、10月、12月是大月，長31日，4月、6月、9月、11月是小月，長為30日，只有2月平年是28日，閏年29日；並且在儒略曆的基礎上改進了閏年的方法，規定凡公元年數被4整除的年份是閏年，但當公元年數是整百整千的“世紀年”時，必須能被400整除的年份才是閏年。每年設365日，閏年為366日。

（二）乾支紀日法的內容和由來

乾支紀日法是漢民族使用天干地支記錄日序的方法，是農曆的一部份，也是歷代曆書的重要組成。乾支是天干、地支的合稱，天干有十：甲、乙、丙、丁、戊、己、庚、辛、壬、癸；地支有十二:子、醜、寅、卯、辰、巳、午、未、申、酉、戌、亥。乾支紀日法使用乾支依次組合的六十甲子來記錄日序，從甲子開始到癸亥結束，六十天為一周，循環記錄。日乾支即是日柱。

乾支紀日法從商朝開始使用，甲骨文字中已有乾支象形。現已考證:春秋以來的乾支紀日從未錯亂過。乾支紀日法是商朝曆法的最大成就，是現今已知世界上最長的紀日法，也是中國一份珍貴的科學文化遺產。

（三）乾支表

把乾支依次組合正好六十為一周，周而復始，循環記錄，這就是俗稱的“乾支表”。乾支表的最大作用就是直觀地列出六十甲子及其對應序列數，這在實際運用中十分重要。使用乾支紀法來表示四柱，即年柱、月柱、日柱、時柱。四柱就是俗語所說的生辰八字。例如：1949年10月1日14時，即可用乾支紀法表示為：己丑年 癸酉月 甲子日 辛未時。則當時出生的嬰兒的生辰八字就是己丑 癸酉 甲子 辛未。

現列十天干、十二地支和乾支表如下:

表1-1十天干

1	2	3	4	5	6	7	8	9	10
甲	乙	丙	丁	戊	己	庚	辛	壬	癸

表1-2十二地支

1	2	3	4	5	6	7	8	9	10	11	12
子	醜	寅	卯	辰	巳	午	未	申	酉	戌	亥

表1-3乾支表

1	2	3	4	5	6	7	8	9	10	11	12
甲子	乙丑	丙寅	丁卯	戊辰	己巳	庚午	辛未	壬申	癸酉	甲戌	乙亥
13	14	15	16	17	18	19	20	21	22	23	24
丙子	丁丑	戊寅	己卯	庚辰	辛巳	壬午	癸未	甲申	乙酉	丙戌	丁亥
25	26	27	28	29	30	31	32	33	34	35	36
戊子	己丑	庚寅	辛卯	壬辰	癸巳	甲午	乙未	丙申	丁酉	戊戌	己亥
37	38	39	40	41	42	43	44	45	46	47	48
庚子	辛丑	壬寅	癸卯	甲辰	乙巳	丙午	丁未	戊申	己酉	庚戌	辛亥
49	50	51	52	53	54	55	56	57	58	59	60
壬子	癸丑	甲寅	乙卯	丙辰	丁巳	戊午	己未	庚申	辛酉	壬戌	癸亥

二、高氏日柱公式

（一）公式

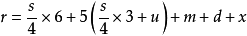
（二）符號意義

r：日柱的母數，r 除以60的餘數即是日柱的乾支序列數；

s：公元年數後兩位數，取整數部分；

u：s 除以4的餘數；

m：月基數

d：日期數

x：世紀常數

（三）世紀常數

世紀常數x是高氏日柱公式中重要的數值。高氏日柱公式以世紀為運算區間，僅取公元年數後兩位代入運算，極大地簡化了日柱求解過程。以世紀為區間進行運算時，每個世紀的日柱初始值必然不同，設日柱初始值為世紀常數x。

關於世紀常數的性質和意義，作出以下兩點說明：

（1）每世紀的第一年是從“0”開始的，故整百整千的“世紀年”即為每世紀的第一年。即例如：1900年應視為20世紀的第1年，其公元年份後兩位為零，即s=0。

（2）世紀常數x即為每世紀第一年3月1日的的日柱序列數減1（由於月基數改良後，將每年3月視為本年的起始月），即例如:21世紀的世紀常數即為2000年的3月1日的日柱序列數減1，而2000年3月1日是戊午日，“戊午”的序列數是55，故x=55－1=54（由於乾支計數的60循環，而54－60=－6，從計算角度來看54與－6是等價的）。

現將17世紀至26世紀一千年間的世紀常數x，對應列表如下：

表2-1.1

世紀數N	17	18	19	20	21
年限	1600-1699	1700-1799	1800-1899	1900-1999	2000-2099
世紀常數x	－3	41	25	9	－6

表2-1.2

世紀數N	22	23	24	25	26
年限	2100-2199	2200-2299	2300-2399	2400-2499	2500-2599
世紀常數x	38	22	6	－9	35

（四）月基數

月基數m，即為一年中當月之前各月的日數總和除以60的餘數。

為了簡化閏日變數的複雜性，增強月基數表的規律性，採用將閏日置後的方式進行求解。由於所有的閏日都加設在每個閏年的2月末尾，故可以採用將2月視為上一年的末月（即14月）的方法，以消除閏日在日柱計算中的複雜插入。相應地，須將1月視為上一年的13月，而將每年的3月份視為本年的起始月（即3月月基數為0）。[4]

現將改進的月基數表列出如下：

表2-2月基數表

單數月	3	5	7	9	11	13
月基數m	0	1	2	4	5	6
雙數月	4	6	8	10	12	14
月基數m	31	32	33	34	35	37

三、公式套用舉例

例1：計算2008年的2月29日的當日日柱，在計算中應將這天視為2008年的14月29日。則有s=7；u=3；m=37；d=29；x=54，將各項數據代入高氏日柱公式可得：

r=1×6+5×(1×3+3)+37+29+54=156

故156除以60餘數為36，即當日日柱為己亥。

例2:計算1949年10月1日即建國當日的日柱，則有s=49；u=1；m=34；d=1；x=9，將各項數據代入高氏日柱公式可得：

r=12*6+5*(12*3+1)+34+1+9=301

故301除以60的餘數為1，即當日的日柱為甲子。

例3:計算2008年5月12日即汶川地震當日的日柱，則有s=8；u=0；m=1；d=12；x=54，將各項數據代入高氏日柱公式可得：

r=2*6+5*(2*3)+2+12+54=109

故109除以60的餘數為49，即當日的日柱為壬子。

例4:計算1895年4月17日即馬關條約簽訂當日的日柱，則有s=95；u=3；m=31；d=17；x=25，將各項數據代入高氏日柱公式可得：

r=23*6+5*(23*3+3)+31+17+25=571

故571除以60的餘數為31,即當日的日柱為甲午。

例5：計算2015年的1月10日的當日日柱，在計算中應將這天視為2014年的13月10日。則有s=14；u=2；m=6；d=10；x=54，將各項數據代入高氏日柱公式可得：

r=3×6+5×(3×3+2)+6+10+54=143

故143除以60餘數為23，即當日日柱為丙戌。

四、結論與擴展

《高氏日柱公式》的成功之處在於：以世紀為運算區間，並引入了世紀常數這一重要的概念。使得日柱的求解在兩位數以內進行，極大地簡化了求解日柱的過程，實現了編寫計算代碼的可行性，且能夠運用於心算。是日柱求解方法的一大創舉和進步。月基數的引入也在很大程度上簡化了求解日柱的過程。經過進一步研究，作者發現世紀常數和世紀年數之間也存在著對應關係，其關係公式（高氏日柱公式的輔助公式）如下：

X=44C+C/4+9，―X=16C―C/4―9

說明：C為公元年數前兩位，X為世紀常數的母數。為世紀推移後同一月日的乾支係數推移。C/4為世紀閏年額外天數（取整）。9為公元元年三月一日乾支係數。X除以60的餘數即為世紀常數x。當求出的世紀常數數值較大時，為了簡化計算，可以利用乾支計數的循環特性進行等價替換（-16C/44C）。

事實上，高氏日柱公式的效力（即適用時間範圍）是與格里曆相同的。而標準的格里曆頒布時間為1582年，並對此前的儒略曆進行了日期刪減，導致了階段日期的不連續。也就是說，格里曆的在1582年是沒有效力的。簡言之，即使從文獻上查得，例如：1492年10月12日哥倫布發現新大陸的日期，也無法用公式準確計算出當日的日柱。當然不是說無法得知，而是需要對方程參數進行適應性修改（重複的11天），蔡勒公式也受此影響。

五、參考文獻

[1]格里曆．中文百科_全球最大中文百科全書[引用日期2015-11-5]

[2]戴興華、楊敏．天干地支的源流與套用．氣象出版社，2006年

[3]雅瑟．中華萬年曆全書．新世界出版社，2011年

[4]蔡勒．蔡勒公式．中文百科[引用日期2015-11-5]