【斜足】:一條直線和一個平面相交且不垂直,那么斜線和平面的相交點叫做斜足。
基本介紹
- 中文名:斜足
- 所屬學科:數學
定義,例題,問題,答案,
定義
空間內一條直線和一個平面相交且不垂直(垂直),那么該斜線和平面的相交點叫做斜足(垂足)。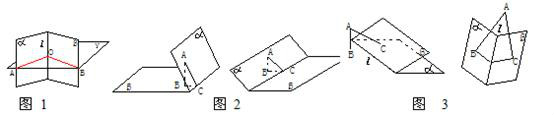

斜足
例題
問題
AC是平面a的斜線, C是斜足,AB垂直a於B,CD在a內,若角ACD=60,角BCD=45,則AC和平面a所成的角等於?
答案
解:過B做BD⊥CD,D為垂足。則: BD=CD,BC=(√2)BD 設BD=CD=m,則BC=(√2)m 因為:AB⊥平面a,BD⊥CD 所以:AD⊥CD (三垂線定理)而:∠ACD=60° 所以:AD=(√3)m 在直角三角形ABD中,由勾股定理求得AB=(√2)m 所以:在直角三角形ABC中,AB=BC=(√2)m知,∠ACB=45° 而:∠ACB就是AC和平面a所成的角所以:∠ACB就是AC和平面a所成的角是45°
