數學地圖學,是研究地圖數學基礎的建立與數學方法的套用。
隨著地圖科學的發展,為了加強地圖學與數學的聯繫,或者說地圖製圖技術要吸取大量的數學方法。同時,關於地圖投影(或原稱數學製圖學)的內容已經顯得狹窄,不能適應地圖科學的發展要求。提出把“數學地圖學”的內容加以擴展和提出與時代相適應的任務是有必要的。
基本介紹
- 中文名:數學地圖學
- 外文名:mathematical cartography
- 學科:測繪科學
- 目的:建立地圖的數學模式
提出,主要內容,任務,總結,
提出
地圖製圖學的歷史發展進程,象其他學科一樣,隨著整個人類生產活動的歷史發展而進步。地圖以有了嚴密的數學基礎而成為科學作品,使它同一般的寫景圖畫有了本質的區別。
不少古代的地圖學家,以創立地圖的某種數學依據(地圖投影)而聞名,如眾所周知的墨卡托、托勒密等尤為著名。我國晉代的地圖學家裴秀,亦以提出了富有數學涵義的製圖六體使製圖技術方法有科學依據而在世界上享有盛譽,例如Herrmann認為裴秀可以和托勒密相提並論。在那時已經出現了矩形格線製圖法。事實上,隨著時代的進步,任何一個學科,都以日益廣泛地運用數學方法而獲得迅速發展,其速度是舊時代所不能想像的。
如果說,傳統的地圖製圖學主要是在建立地圖數學基礎方面運用了較多和較複雜的數學方法,而在其它階段明顯的比較少,那末在地圖製圖學發展到自動化製圖的階段中,一定要大大地增加數學方法的運用。這是地圖製圖技術從傳統的方式轉變到自動製圖的必然規律。
國際製圖協會曾提到要解決人類面臨的三大問題(即生產力的合理配置、自然資源的合理使用以及與自然作鬥爭),需要大量的現代地圖,估計每天要出版上千幅地形圖,加上各種專題圖,則為數更大,沒有自動化製圖要完成這一任務是難以達成的。
要發展自動化製圖,一個基本問題是解決地圖製作過程的數學描述,或者稱之為建立地圖的數學模式。這是地圖製圖工作者面臨的新任務。
過去二十年,地圖製圖專業中建立地圖數學基礎的一個專門分支科目在專業教育中是作為“地圖投影”一門課程出現的。或者推而廣之加進了一部分地圖量算內容而稱為“數學製圖學”,看來隨著地圖科學的發展,為了加強地圖學與數學的聯繫,或者說地圖製圖技術要吸取大量的數學方法,有必要擴展“數學地圖學"這一專業科目。(在外文中這一科目名稱都很一致,例如英語為“Mathematical Cartography”,在中文中為更明確,似宜稱為“數學地圖學”)。
在國外,以東德德勒斯登工業大學地圖製圖專業新教學計畫為例,反映了這一發展趨勢,其中一門“Mathematische Kartographie”包含了三部分內容,為球面三角、地圖投影、數理統計。另一門新課程是“電子數位化處理與自動化基礎”,前後延續達五個學期之久,這顯然包含著許多基本的數學方法。
在宇航飛行器對地球和其他星球的攝影成果質量日益提高的情況下;顯示了這種資料對於地球的專題製圖和其他星球製圖的巨大可能性,為此要解決宇航攝影資料用於製圖目的的數學處理。其任務是宇航像片的空間定位和轉換地圖投影。而對於其他星球,則要設計適宜的星球圖投影。
以上例子說明了原來關於地圖投影(或原稱數學製圖學)的內容已經顯得狹窄,不能適應地圖科學的發展要求。因此,提出把“數學地圖學”的內容加以擴展和提出與時代相適應的任務是有必要的。
主要內容
研究地圖數學基礎的建立與數學的套用。主要包括:
①地圖投影理論,即地圖投影的設計原理,常用投影的標準化及投影變換的數學方法;
②地圖的各種數學模式;
③地圖概括中數理統計原理與方法;
④表示數量特徵的地圖(如等值線圖、統計地圖)、評價地圖、預報地圖、合成地圖的數學原理;
⑤地圖量算的數學方法;
⑥計算機製圖的數學原理與方法;
⑦地圖套用的各種數理統計方法與數學模型的建立。
其中地圖投影理論已有較深入研究,數理統計方法、地圖量算、機助製圖數學方法的套用也有較好基礎,地圖套用的數學方法有待深入研究。
任務
國外認為當前有下列任務:建立合理的地圖投影命名系統,研究地圖投影標準化原則,編輯地圖投影集,解決數學製圖學的新問題,用航天攝影測制地圖時的地圖投影問題以及其他星球測圖的投影問題,探索新的地圖投影以及研究和完善地圖圖形的糾正方法。
除了上述這些任務之外,下面我們從各方面列舉一些內容或發展的現狀來談談“數學地圖學”,可能擴展的內容。
建立合理的地圖投影命名系統
這是地圖投影的基本理論問題之一,也就是恰當地解決分類系統問題。迄今不是沿用舊有分類就是不夠完備化,而且邏輯性不強,或者缺乏從本質上的分析,而使問題逗留在舊的範疇中。地圖投影的分類,有內在和外在的不同標誌。內在的是屬於本質的(如按變形性質),外在的標誌是經緯網形狀,而這後者是一定條件下(例如正軸投影)才具有的特徵。
對於地圖分類系統的研究
從變形橢圓的本質上來分析,或者說,分析變形橢圓有無等長方向作為基本的赳分是適宜的。這樣最初的基本劃分將可分為橢圓型投影(任一點處皆無任何等長方向)——等角投影即包含於其中;拋物型投影(任一點處都有唯一的等長方向)——等距離投影即屬於此;雙曲型投影(任一點處都有二不同的等長方向)——等面積投影包含於其中。這三大類別的關係如下圖所示,有斜線的部分是橢圓型投影範疇(A),a=1或b=1的兩條線代表了拋物型投影;空白部分是雙曲型投影範疇(B)。

由圖可見,連線原點0與(1,1)的直線是直角的分角線(a=b),代表了等角投影。在(B)域中過(1,1)的雙曲線ab=1代表了等面積投影。代表等距離投影a=1或b=1的直線是(A)與(B)兩個區域的分界。分別位於(A)域或(B)域的線條代表的投影以及等距離投影是屬於單純的投影。穿越(A)、 (B)兩個區域的線條(如上圖中的l),則是某種混合投影。這種新的分類,將是一種較合乎邏輯的分類法。值得結合地圖投影的實踐來深入研究。
隨著製圖自動化的發展,擺在“數學地圖學”面前的一個迫切任務是解決地圖投影的交換問題。不解決這個問題,除了系列性地圖(如地形圖)的相似變換外,不同投影,特別是變形性質與形狀差別較大的地圖資料與所編圖投影之間自動轉繪是不可能的。這就要解決起始地圖投影



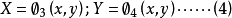
上列方程的解法,只是對個別投影進行過研究。對於大多數投影要確定地理坐標對直角坐標的精確解析關係困難甚大或者是不可能的。為此不同學者考慮了幾種不同的方法。例如在兩種投影直角坐標之間建立直接聯繫,即把X、Y寫成x、y的多項式,以及用最小二乘法逼近和分步解法等。究竟哪種情況下為可能,哪種情況下為不可能,這就要加以研究。也就是說尋求既適用於一定區域範圍,又能保證一定精度的近似解法是很重要的課題。
從地圖製圖自動化三個基本階段(即資料收集與數位化階段、資料處理階段、自動繪圖階段)看來,第二階段的關鍵問題實質上是製圖綜合的自動化。實際上,製圖綜合乃是一種最優逼近而且它是可以用數學最佳化模式來表述的。就綜合過程而言,它包含著若干部分的處理過程,即地圖物體的選取、圖形的組合、質量的合併、化簡與位移。這些過程是互相依存和互相制約的。這就使得建立綜合模式非常複雜,迄今還沒有可套用的製圖綜合的完整模式。目前存在一些可用的部分解決方法。例如Topfer的根式規律

常用於物體的選取。這個規律在不同國家製圖綜合理論與實踐中均得到較廣泛的使用。但不同情況下要補充以適當的係數和予以完善。又如在曲線化簡方面,要用到不同的光滑化的算法,以至用到濾波理論,在點的化簡中要用到“凝聚”方法。這些都要運用逼近理論中的最優估計。也許製圖綜合理論可以用模糊數學來表述。
對於大量地圖信息的預先處理,眾所周知,要運用機率論和數理統計方法。
地圖是各種信息的集合。在總的集合中,可以分割成許多子集合。研究製圖物體和現象的分布的數學模式,實際上就是集合代數的運算,可用以抽象地表達不同比例尺地圖上信息的相互關係。
要解決由地形圖多方面的用途以及因此引起的各種不同用圖者對地圖提出的具有矛盾性的要求,這就要求編輯、編圖人員運用對策論來研究。有的文獻中還提到要運用控制論、拓撲學、圖論等基本理論以建立地圖的數學模式。
總結
在地圖的實際套用方面,地圖的量算技術,特別是連繫到現代計算機和數位化器的運用,要研究各種數據的量算方法。也要研究不具備上述設備的條件下, “常規”的地圖量算方法。
總之,地圖學作為地理和測繪學科的結合部,隨著電子技術的發展,已到了突變的階段。雖然全部自動的編繪技術還是在實驗階段,但光輝的前景已經展示在前面。地圖製圖工作者要有足夠的思想認識,同時要有基本理論的準備。這就是要學習、研究和充分運用數學的基本方法,特別是在專業教學計畫中要加強數學基礎課。相應地,在專業課中要使“數學地圖學”的內容,豐富到足以適應時代的要求。這當然不是說,要把現代地圖科學內容都容納到原來的一門科目中,那是不可能的。但是把“數學地圖學”從原來局限的內容適當地加以擴展很有必要。根據上面列舉的一些數學方法在地圖製圖學中的運用,是否可以提出以下一些新的內容和任務:
為宇航資料套用於地圖製圖解決空間定位和攝影變換問題;
用於地圖資料處理的數理統計的基本方法;
建立地圖模式的數學方法的探索;
地圖綜合自動化的數學理論基礎;
集合代數、資訊理論等數學分支用於理論製圖學的基本原理,等等。
至於從屬於原來“地圖投影”範疇的內容就不列舉了。
這裡提出的是處在當前地圖製圖科學的發展要求很高而現實的地圖專業教育和科學研究落後於形勢的情況下,對一個科目內容向廣度、深度發展的一些看法。顯然,隨著專業科學水平的提高,形成一個新的專業基礎科目(假定說“地圖製圖數學原理”),也並不是意外的事。

