正平面直角坐標系內,橫坐標、縱坐標都是整數的點稱為整點。在數學競賽試題中,常涉及整點問題,或討論以整點為頂點的平面圖形的存在性,或討論涉及整點的平面圖形的性質,或計算平面區域內含整點的個數,或套用整點知識來解決其他相關問題等。
整點問題通常可以用鴿巢原理來進行求解。
基本介紹
- 中文名:整點問題
- 外文名:lattice-point problem
例1
例2

例3
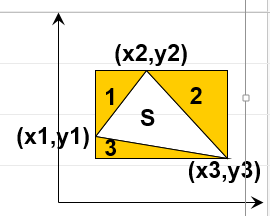
例4
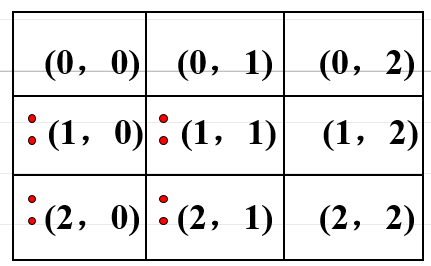

正平面直角坐標系內,橫坐標、縱坐標都是整數的點稱為整點。在數學競賽試題中,常涉及整點問題,或討論以整點為頂點的平面圖形的存在性,或討論涉及整點的平面圖形的性質,或計算平面區域內含整點的個數,或套用整點知識來解決其他相關問題等。
整點問題通常可以用鴿巢原理來進行求解。




正平面直角坐標系內,橫坐標、縱坐標都是整數的點稱為整點。在數學競賽試題中,常涉及整點問題,或討論以整點為頂點的平面圖形的存在性,或討論涉及整點的平面圖形...
格點,又稱整點,指坐標都是整數的點,格點問題就是研究一些特殊區域甚至一般區域中的格點的個數的問題。...
《數學的100個基本問題》是 2004年1月1日山西科學技術出版社出版的圖書,作者是...022 華林問題023 多邊形數024 巴赫猜想025 生素數猜想026 圓內整點問題...
[6]山東省自然科學基金:1999.01—2001.12,指數和估計與整點問題(主持)。詞條標籤: 行業人物 , 教育, 教師, 大學教師 , 人物, 書籍 ...
二元二次不定方程本質上可以歸結為求二次曲線(即圓錐曲線)的有理點或整點問題。...... 次不定方程本質上可以歸結為求二次曲線(即圓錐曲線)的有理點或整點...
作者把華林問題與哥德巴赫問題的研究方法結合起來,並把華林問題一方面推廣到每一加數是整係數多項式的情形,一方面限制變數僅取素數值。作者把塔銳問題也加上了變數...
《數論經典著作系列:解析數論基礎(第2版)》以解析數論的四個著名問題:平面區域內的整點問題、素數分布問題、Goldbach問題和Waring問題為中心,很好地闡明了解析數論的...
在圓內整點問題,球內整點問題,華林問題,三維除數問題等等之上,他都改進了中外數學家的結果。單是這一些成果,他那貢獻就已經很大了。...
數學上把在平面直角坐標系中橫縱坐標均為整數的點稱為格點(lattice point)或整點。坐標平面內頂點為格點的三角形稱為格點三角形,類似地也有格點多邊形的概念。...
