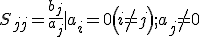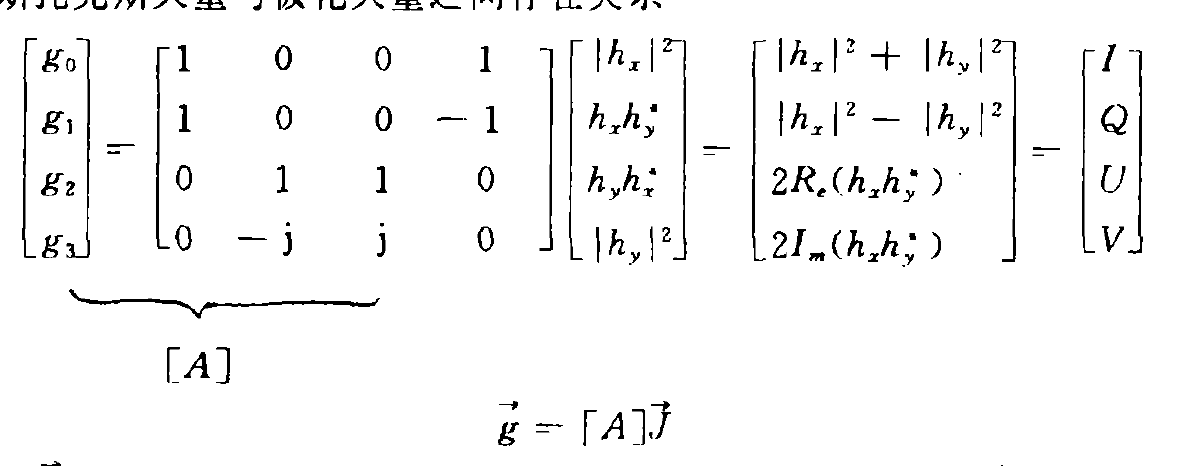散射矩陣

散射矩陣是物理學中描述散射過程的一個主要觀測量。

假設散射源為很好的定域散射源，與被散射粒子的相互作用局限在有限的空間範圍內，那么，無窮遠時間以前粒子處於一個自由態，稱為入態，無窮遠時間之後粒子也是處於一個自由態，稱為出態， 入態到初態，相互作用可以用一個矩陣描述，記為S，那么就有|Ψ>out=S |Ψ>in。這就是散射矩陣的定義。

基本介紹

• 中文名：散射矩陣
• 外文名：scattering matrix
• 別名：S矩陣 
• 所屬學科：物理
• 實質：描述散射過程的一個主要觀測量
• 兩種典型矩陣：辛克萊散射矩陣、米勒散射矩陣

概念闡釋

定義

假設散射源為很好的定域散射源，與被散射粒子的相互作用局限在有限的空間範圍內，那么，無窮遠時間以前粒子處於一個自由態，稱為入態，記為|Ψ>in；無窮遠時間之後粒子也是處於一個自由態，稱為出態，記為 |Ψ>out。 入態到初態，相互作用可以用一個矩陣描述，記為S，那么就有：

|Ψ>out=S |Ψ>in

這就是散射矩陣的定義。現代高能物理的發展，同其他物理學一樣是理論和實驗的互動，而這種互動主要的橋樑就是散射矩陣。

散射矩陣直接與可觀測的物理量相聯繫，但是我們在量子場論中處理的是場，利用一個LSZ約化規則，它聯繫了量子場論中的格林函式和可觀測的散射矩陣。這使得理論能夠預言實驗。

在微波元件中的定義

散射矩陣在微波元件中表示網路特性的參量之一，在n連線埠線性網路中，描述各連線埠歸一化入射電壓波a與歸一化反射電壓波b之間的關係為[b]=[S][a]，其中[S]稱為散射矩陣，各矩陣元素S_ij稱為散射參量，其優點是在微波網路中便於測量，且有

S_jj和S_ij分別表示除第j連線埠接信號源其餘連線埠全部接匹配負載時，第j連線埠的歸一化電壓反射係數和從第j連線埠到第i連線埠的歸一化電壓傳輸係數。

兩種極化散射矩陣

辛克萊散射矩陣

在雷達目標散射問題中, 散射矩陣完整地體現了人射電磁場矢量與散射電磁場矢量之間的關係。實際系統中, 入射電磁場來源乾雷達發射機, 而散射電磁場則由雷達目標散射產生並為雷達接收機所接收。我們知道, 散射矩陣的確定與收發系統的配置無關, 因此它包含的僅是雷達目標的信息, 體現的僅是雷達目標的特性。

由於任意雷達目標的散射矩陣都可以通過測量得到, 所以通過研究各種目標的散射矩陣就可得到這些目標的散射特性。現有的研究成果表明, 雷達目標的橫截面積對於入射電磁場的極化狀態是很敏感的, 我們可以將任何目標均視為一個極化變換器, 而散射矩陣正好描述了該目標的極化變換特性。

如果用[S] _SMA 表示含絕對相位的辛克萊散射矩陣, 用[S]_SMA表示含相對相位的辛克萊散射矩陣, 則

米勒散射矩陣

當我們用斯托克斯( S ot k e s )矢量來描述電磁波的極化狀態時, 目標的極化散射矩陣為米勒矩陣。此時雷達目標的極化變換效應可用性4*4 在米勒矩陣來加以描述, 值得注意, 該矩陣的所有陣元均為實數

我們根據描述入射場極化矢量與散射場極化矢量之間關係的辛克萊散射矩陣[S]可以求得米勒矩陣的各個實陣元。我們知道斯托克斯矢量與極化矢量之間存在關係

即可得到米勒矩陣[M]與辛克萊矩陣[S]之間的關係式

測量方法

通常極化散射矩陣的測量是利用專用的測量雷達，分時測量得到的。

目前方法一是利用專用的極化測量雷達，在兩個正交極化通道上，同時發射兩個正交極化E_x、E_y，(如果E_x=E_y，其合成矢量就是一個夾角為45°的線極化)，然後，通過信號編碼的方法，來完成極化矩陣的“同時性”測量。其成功之處在於解決了極化測量雷達的兩大問題。一是打破了快速極化開關給測量精度度帶來的誤差；二是消除了由轉換開關造成的脈間相位和幅度的不穩定性所帶來的誤差。

但是，這種測量方法不可避免的存在兩個小小的不足：①同時發射的E_x、E_y，在空間合成後，乃至入射到目標上，它仍是一個斜線極化波，因此所得到的散矩陣實際上是一個由線極化入射產生的、極化基旋轉了45 °後的變換矩陣而已，它得不到完整散射特性。②它需要專門的測量雷達。由於極化信息處理利用日益廣泛，往往要求在值班極化雷達上，對目標散射矩陣進行線上實時測量，而不是另加測量雷達。

方法二是利用相對極化矩陣的測量框圖及其原理，但測量方法仍是分時進行的。由於目標通常指運動目標，散射矩陣隨目標姿態變化而變化，這就要求我們對散射矩陣進行實時測量，才能達到欲完成的控制目的。正是基於這種考慮，利用正在值班(擔負任務)的極化捷變雷達，對散射矩陣進行實時測量，是本文的貢獻。歸納起來講，①利用正在值班的極化雷達，而不是另配極化測量雷達；②對散射矩陣進行實時測量，以達到實時控制的目的。