支撐子圖(spanning subgraph)亦稱生成子圖,圖論中一類圖的統稱。由一個圖的全部頂點及連結這些頂點的部分邊構成的圖稱為原圖的支撐子圖。若支撐子圖是樹,則為支撐樹。在圖論中,解決一些懸而未決的問題往往首先從樹這類圖入手。許多問題對一般的圖未能解決或者沒有簡便的方法,而對於樹,則已完滿解決,且方法較為簡便。
基本介紹
- 中文名:支撐子圖
- 外文名:spanning subgraph
- 同義詞:生成子圖
- 領域:計算機科學
- 分類:圖論
- 相關:支撐樹
概述,定義,定理1及證明,定理2及證明,
概述
由一個圖的全部頂點及連結這些頂點的部分邊構成的連通圖稱為原圖的支撐子圖。給定連通圖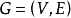 ,若
,若 ,
,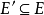 ,則稱圖
,則稱圖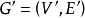 是由
是由 生成的部分圖,記為
生成的部分圖,記為 ,而當
,而當 是連通的(任意兩個頂點之間至少有一通路連線),稱
是連通的(任意兩個頂點之間至少有一通路連線),稱 是
是 的支撐子圖。也即連通圖
的支撐子圖。也即連通圖 的支撐子圖
的支撐子圖 包含
包含 的所有頂點,並且是連通的。
的所有頂點,並且是連通的。
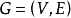

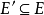
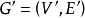








給定一個無向圖 ,若
,若 的一個支撐子圖
的一個支撐子圖 是樹,則稱
是樹,則稱 為
為 的支撐樹。圖的支撐樹不是唯一的。但任何連通圖至少有一顆支撐樹。所有支撐樹中具有最小數的支撐樹稱為最小支撐樹,求最小支撐樹是實際問題的需要,例如“為了把若干城市連線起來,設計最短通信線路”,“為了解決若干居民點供水,要求設計最短的自來水管線路”等等。
的支撐樹。圖的支撐樹不是唯一的。但任何連通圖至少有一顆支撐樹。所有支撐樹中具有最小數的支撐樹稱為最小支撐樹,求最小支撐樹是實際問題的需要,例如“為了把若干城市連線起來,設計最短通信線路”,“為了解決若干居民點供水,要求設計最短的自來水管線路”等等。





定義
定義1 設 為
為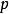 個頂和
個頂和 個邊的任意連通圖,則
個邊的任意連通圖,則 中任意
中任意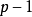 個邊所導出的
個邊所導出的 個子圖稱為支撐子圖。
個子圖稱為支撐子圖。

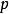


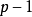

定義2 設圖 中存在
中存在 個支撐子圖,則
個支撐子圖,則 個支撐子圖中
個支撐子圖中 個不含圈的支撐子圖稱為支撐樹,
個不含圈的支撐子圖稱為支撐樹,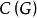 個含圈的支撐子圖稱為含圈的支撐子圖,並有
個含圈的支撐子圖稱為含圈的支撐子圖,並有 。
。




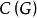

定理1及證明
定理1 設 為任意連通圖,則
為任意連通圖,則 中任意
中任意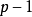 個邊所導出的支撐子圖的個數為
個邊所導出的支撐子圖的個數為


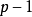


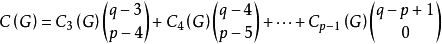

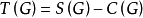
式中: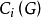 為圖
為圖 中
中 的個數;
的個數;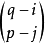 為
為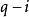 個邊中任取
個邊中任取 個邊的選擇數。
個邊的選擇數。
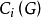


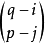
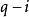

證明:不失一般性,設 為
為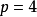 ,
,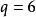 的完全圖
的完全圖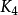 ,且
,且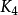 中
中 的個數
的個數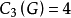 ;
; 的個數
的個數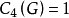 ,若定理1為真,則
,若定理1為真,則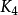 中
中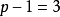 個邊所導出的支撐子圖的個數
個邊所導出的支撐子圖的個數

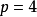
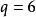
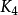
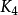

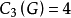

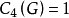
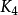
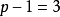






定理1得證。
定理2及證明
定理2 設 為任意連通圖,則
為任意連通圖,則 中
中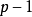 個邊所導出的
個邊所導出的 個支撐子圖的構造歸結為
個支撐子圖的構造歸結為


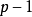


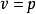
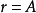
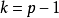
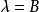








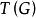
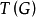

證明:不失一般性,設 為
為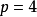 ,
,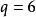 的完全圖
的完全圖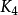 ,若定理2為真,則完全圖
,若定理2為真,則完全圖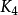 的
的 個生成子圖的構造歸結為
個生成子圖的構造歸結為 ,
, ,
,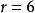 ,
, ,
, 的
的 設計中下列20個區組:
設計中下列20個區組:

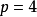
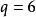
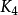
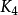



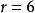




(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,3,4),(1,3,5),(1,3,6),(1,4,5),(1,4,6),(1,5,6),(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6),(3,4,5),(3,4,6),(3,5,6),(4,5,6)的構造,當中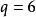 個邊的編號被確定後,
個邊的編號被確定後, 個支撐子圖與20個區組一一對應,20個支撐子圖中有4個含圈的支撐子圖,有16個不含圈的支撐子圖(支撐樹)。亦即:
個支撐子圖與20個區組一一對應,20個支撐子圖中有4個含圈的支撐子圖,有16個不含圈的支撐子圖(支撐樹)。亦即: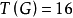 ,
, 且
且 ,見圖1。
,見圖1。
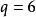

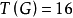


定理2得證。
