擺渡問題

擺渡問題(ferry problem)是一類組合最佳化問題，在一條河的一邊岸上有一隻狼、一隻羊和一棵白菜，已知狼吃羊和羊吃白菜，在河中只有一條小舟且每次只能載它們三者之一，問如何用最少的次數將它們安全擺渡到對岸?這就是所謂擺渡問題，也可將它推廣到一般的情形。

基本介紹

• 中文名：擺渡問題
• 外文名：ferry problem
• 所屬學科：數學
• 所屬問題：組合學（組合多最最佳化)
• 簡介：一類組合最佳化問題

基本介紹

中世紀，英國數學家阿爾昆(Alcuin，735-804)在其《益智集》(Problems for the Quickening of the Mind)中提出：有人攜帶一隻狼、一隻羊、一籃白菜渡河。唯一的工具是一條小船。小船一次只能載他自己和三樣東兩中的一樣。如果只留下羊和白菜在一起，羊就會吃掉白菜；如果留下羊和狼在一起，狼就會吃掉羊。問這個人如何安排擺渡，方能使白菜、羊和狼都平安抵達對岸?

可以利用路徑的概念解此問題。

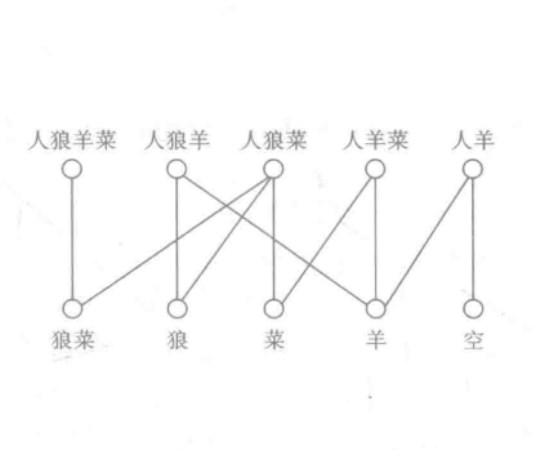
解：河左岸允許出現的情況有以下10種情況：人狼羊菜、人狼羊、人狼菜、人羊菜、人羊、狼菜、狼、菜、羊及窄(各物品已安全渡河)。把這10種狀態視為10個點，若一種狀態通過一次擺渡後變為另一種狀態，則在兩種狀態(點)之間畫一直線，得到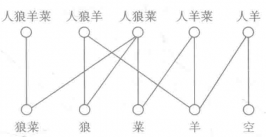圖1。

圖1

這樣擺渡問題就轉化成在圖中找出以“人狼羊菜”為起點，以“空”為終點的簡單路徑。容易看出，只有兩條簡單路徑符合要求，即

(1)人狼羊菜、狼菜、人狼菜、菜、人羊菜、羊、人羊、空：

(2)人狼羊菜、狼菜、人狼菜、狼、人狼羊、羊、人羊、空。

對於簡單路徑(1)的安排為：人帶羊過河；人剛來；帶狼過河；放下狼再將羊帶回；人再帶菜過河；人回來；帶羊過河。

對於簡單路徑(2)的安排為：人帶羊過河；人回來；帶菜過河；放下菜再將羊帶回；人再帶狼過河；人回來；帶羊過河。

上述的兩種方案都是去4次、回3次，且不會再有比這更少次數的渡河辦法了。

擺渡問題的推廣與變形

16世紀，義大利數學家塔塔格里亞(N.Tartaglia，1499-1557)將擺渡問題設計成一個新版本：

三位美麗的新娘和她們愛吃醋的先生一同旅行。他們來到了一條河邊，但只有一條小船，小船一次至多只能載二人。為了避免有人吃醋，他們約定：除非自己的先生在身旁，否則任一女士不得和其他男子在一起。問怎樣安排渡河?

答案是往返1 1次。如果只有兩對夫婦，則往返5次就夠了；如果有四對或更多對夫婦，那么問題無解。該問題後來又被推廣成：

(1)n對夫妻用一條船過河，該船僅可由一人來劃，至多可載 個人，條件仍是任一女士除非自己的先生在身旁，否則不得和其他男子在一起。問至少需要往返幾次?(設擺渡次數為y，則 時， ； 時， ； 時， 。)

(2)問一條船至少能載幾個(X)人時，才能使11對夫妻可乘它渡河，而任一女士除非自己的先生在身邊，否則不得和別的男子在一起；假設船僅可由一人來劃。並求往返擺渡的最小次數(y)。結果見表1。

表1 擺渡問題的解

n	x	y
2	2	5
3	2	11
4	3	9
5	3	11
》5	4	2n-1

與擺渡問題相類似的是火車轉軌問題。圖2中有一火車頭L和兩節貨車車廂 ，DA是 所在側線的公共部分，長度足夠停放 ，但不能同時容下這兩節車廂，也容小下火車頭L。這樣，停在DA上的車廂可以轉軌到側線上。工程師的工作是轉換 的位置。問如何完成?這個問題並不難，但如果有更多的車廂(如在鐵路貨物分類站)，要按車廂目的地先後順序進行排列，那么__：I二程師就需要有很高的數學水平才能完成職責了。