擴張實數系

擴張實數系(extended real number system)是實數加上無窮遠點的集合。擴張的實數系由實數系R¹加進兩個符號﹢∞和﹣∞組成，具有下述性質：(i)若x是實數，則﹣∞<x<﹢∞，且x+∞=﹢∞，x－∞=﹣∞， x/(﹢∞)=x/(﹣∞)=0；(ii) 若x>0，則x·(﹢∞)=﹢∞，x·(﹣∞)=﹣∞；(iii)若x<0，則x·(﹢∞)=﹣∞，x·(﹣∞)=﹢∞。運算∞－∞不定義。所有擴張的實數之集記為R*或R¹_e等，當需要區別實數與符號+∞和﹣∞時，前者叫做是有限的。

基本介紹

• 中文名：擴張實數系
• 外文名：extended real number system
• 所屬學科：數學
• 所屬問題：數學分析
• 簡介：實數加上無窮遠點的集合

基本介紹

擴張實數系是實數加上無窮遠點的集合，把兩個理想點+∞(讀作正無窮大)與﹣∞(讀作負無窮大)加進實數系所得到的數系，通常記為R*或[﹣∞，+∞]。

注 擴張的實數系的一種用途是表達式“supS”，若S是有上界的非空實數集，則定義supS為S的最小上界，若S沒有上界，就定義supS為+∞，於是，對所有非空集S，supS都有定義，而且，如果我們定義空集的上確界是﹣∞，那么無論在何種場合，supS都是大於或等於S的各個元素的最小的擴張實數。關於“infS”採用類似的約定。

擴張實數系的性質

R*的元素滿足以下規定(不同文獻中的提法略有差異)：

1.對任意實數a，有-∞<a<+∞，

a+(±∞)=(±∞)+a=±∞，

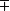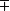a-(±∞)=∞，a/(∞)=0.

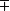
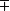
2.(+∞)+(+∞)=+∞，

(-∞)+(-∞)=-∞.

3.若a>0或a=+∞，則a·(±∞)=(±∞)·a=±∞;

若a<0或a=-∞，則a·(±∞)=(±∞)·a=∞.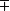

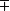
實數系R可以用集合{x|-∞<x<+∞}表示。在數軸上，+∞與-∞分別表示正向與負向的無窮遠點。引進理想元素+∞與-∞，主要是為了敘述與表示上的方便(例如，可以統一處理函式極限)，另一方面，也是為了把R擴張為緊緻集R*(賦予適當的距離後，它與閉線段同胚)。這種緊緻化思想在現代數學中是相當有用的。

若S是R*的非空子集，設supS是R*中對每個x∈S有x≤b的最小的元素b。若+∞∈S，顯然supS=+∞。此外，若對每個x∈S有x<+∞，但S在R內沒有上界，則supS=+∞。

inf S的定義是類似的。所謂+∞的鄰域，是指任一集{x∈R*：x>c}。於是R*內的序列收斂於+∞就變得有意義了。若x₁,x₂,...是R*內的任一不減序列，使對某個m有x_m>-∞，則此序列有極限x₀，x₀可為有限數(即在R內)，可為+∞。