在雙曲線幾何中,理想點,歐米茄點或無窮遠點是雙曲面平面空間外的明確定義點。 給定線l和點P,但點P不在l上,通過點P作l的左右趨近平行線,二者相交於理想點。
與投影不同,理想點形成的是邊界,而不是體內。 儘管這些點定義的位置很好,但是這些線不會在理想點相交,本身也不屬於雙曲線空間。
基本介紹
- 中文名:理想點
- 外文名:Ideal point
- 學科:數學
- 適用場合:雙曲線空間幾何
- 模型表示:克萊恩圓盤模型等
- 相關名詞:理想三角形
定義介紹,屬性,多邊形,理想三角形,理想四邊形,理想正方形,理想正邊形,幾何模型表示,
定義介紹
在雙曲線幾何中,理想點,歐米茄點或無窮遠點是雙曲面平面空間外的明確定義點。 給定線l和點P,但點P不在l上,右和左限制平行於l到p在理想點收斂到l。
與投影不同,理想點形成的是邊界,而不是子體。 因此,儘管這些點定義的位置很好,但是這些線不會在理想點相交,本身也不屬於雙曲線空間。
屬性
理想點與任何其他點或理想點之間的雙曲線距離是無窮大的。
霍爾和霍布斯的中心是理想的點; 當它們具有相同的中心時,兩個環形圈是同心的。
多邊形
理想三角形
如果三角形的所有頂點都是理想點,則三角形是理想的三角形。
理想的三角形有許多有趣的屬性:
(1)所有理想的三角形都是一致的。
(2)理想三角形的內角全部為零。
(3)任何理想的三角形都有無限的周長。
(4)任何理想的三角形具有面積π/ -K,其中K是平面的(負)曲率。
理想四邊形
如果四邊形的所有頂點都是理想點,則三角形是理想的四邊形。
雖然所有理想的三角形都是一致的,但不是所有的四邊形都是,對角線可以彼此形成不同的角度,從而產生不均勻的四邊形:
(1)理想四邊形的內角全部為零。
(2)任何理想的四邊形都有無限周長。
(3)任何理想(凸非交叉)四邊形具有面積2π/ -K,其中K是平面的(負)曲率。
理想正方形
兩個對角線彼此垂直的理想四邊形形成一個理想的正方形。
在費迪南德·卡爾·施維卡特所謂的“星體幾何”的備忘錄中使用了這個概念。 第一個出版物承認雙曲線幾何的可能性。
理想正邊形
由於正邊形可以被細分為(n-2)個理想三角形,區域(n-2)是理想三角形的面積。
幾何模型表示
在克萊因圓盤模型和龐加萊圓盤模型的雙曲面中,理想點在單位圓(雙曲面)或單位球(較高維度)上,這是雙曲面的不可達邊界。
當將相同的雙曲線投射到克萊因圓盤模型和龐加萊圓盤模型時,兩條線都經過相同的兩個理想點(兩個模型的理想點在同一點上)。
克萊恩圓盤模型
給定打開的單位盤中的兩個不同點p和q,連線它們的直線與單位圓相交,為使得點依次為a,p,q,b,在兩個理想點(a和b)中標記,使得|aq| > | ap | 和| pb | > | qb |。 那么p和q之間的雙曲線距離表示為
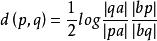
龐加萊圓盤模型
給定打開單位盤中的兩個不同點p和q,則與連線它們的邊界正交的唯一圓與兩個理想點(a和b)中的單位圓相交,使得點依次為a,p, q,b這樣| aq | > | ap | 和| pb | > | qb |。 那么p和q之間的雙曲線距離表示為
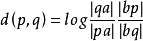
其中沿著(直線)段aq,ap,pb和qb測量距離。
 龐加萊圓盤模型中的三個理想三角形,頂點是理想點
龐加萊圓盤模型中的三個理想三角形,頂點是理想點龐加萊半平面模型
在龐加萊半平面模型中,理想點是邊界上的點,而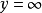 的歐幾里德線是一個理想點。
的歐幾里德線是一個理想點。
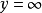
雙曲面模型
在雙曲面模型中,沒有理想點。

