擬基本解(parametrix)微分運算元的基本解的一種近似,格林函式是一種經典的擬基本解。
基本介紹
- 中文名:擬基本解
- 外文名:left(right)parametrix
- 適用範圍:數理科學
定義
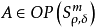
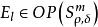
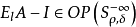
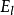
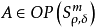
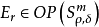
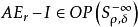
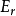
基本解
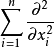
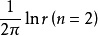
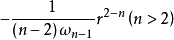
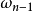
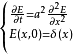
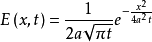
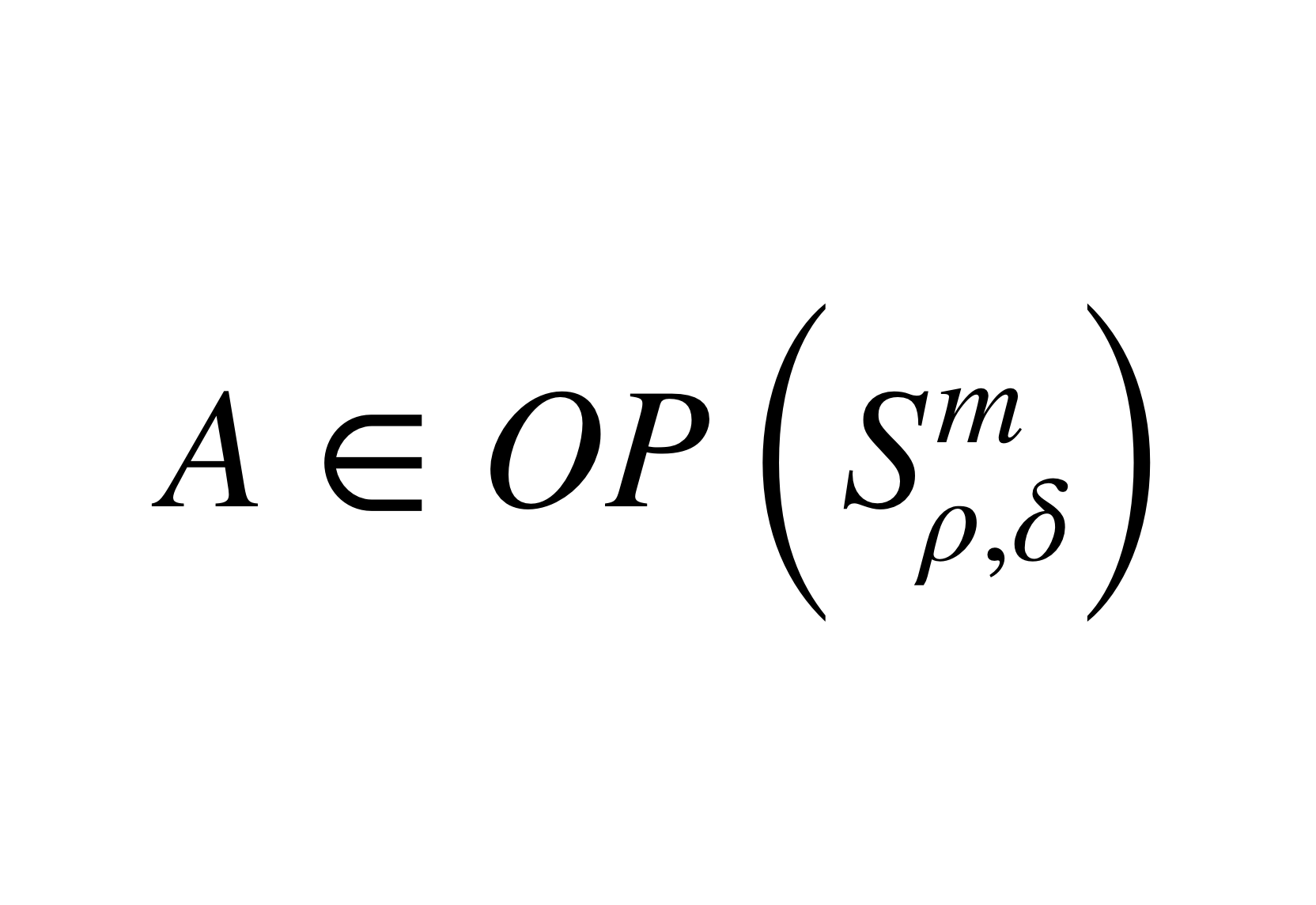
擬基本解(parametrix)微分運算元的基本解的一種近似,格林函式是一種經典的擬基本解。
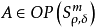
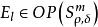
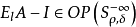
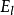
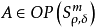
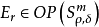
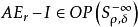
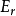
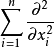
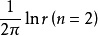
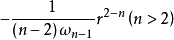
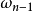
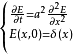
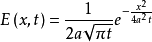
擬基本解(parametrix)微分運算元的基本解的一種近似,格林函式是一種經典的擬基本解。...... 擬基本解(parametrix)微分運算元的基本解的一種近似,格林函式是一種經典...
概念定義 擬基本解存在定理(existence theorem of the parametrix)判斷橢圓型擬微分運算元有擬基本解 的定理.如果Q E OPS'"為恰當支的橢圓型擬微分 運算元,那么存在...
有限基本解法 (method of finite fundamental solutions)解線性勢流動的一種數值計算方法,它用一些形式比較簡單、而在流動區域內又滿足方程的解析函式(如位勢流的源...
《模擬電子技術基本教程習題解答》是華成英主編的《模擬電子技術基本教程》(普通高等教育“十一五”國家級規劃教材,清華大學出版社2006年出版)的配套輔導書。《模擬...
《模擬電子技術基本教程》是由清華大學出版社出版編著的實體書。主要內容包括,模擬電子系統簡介、集成運算放大電路及其基本套用、半導體二極體及其基本套用電路、晶體...
nǐ dìng擬定基本解釋 編輯 1、[work out]:草定。擬定計畫。擬定試題。...2、決定;擬測事情且做確定。元無名氏 《舉案齊眉》第一折:“我又不會臨邛...
侔擬,讀音móu nǐ,漢語詞語。類似,相同。中文名 侔擬 基本解釋 類似,相同 拼音 móu nǐ 詞性 名詞目錄 1 基本解釋 2 詞語分開解釋 ...
虛擬基本解釋 1. [unreal]∶不符合或不一定符合事實的虛擬的情況2. [fictitious;invented]∶憑想像編造的事物3.由高科技術實現的仿實物或偽實物的技術...
語出《易·繫辭上》:“擬之而後言,議之而後動,擬議以成其變化。”...1 基本解釋 2 引證解釋 擬議基本解釋 編輯 1. 行動之前的計畫、籌劃。2...
基本解釋 一款簡單好玩的恐龍模擬遊戲 目錄 1 基本信息 2 遊戲介紹 3 遊戲圖冊 霸王龍模擬基本信息 編輯 遊戲名:霸王龍模擬 [1] 遊戲...
沙盤模擬基本介紹 編輯 模擬沙盤各職能中心涵蓋了企業運營的所有關鍵環節:戰略規劃、資金籌集、市場行銷、產品研發、生產組織、物資採購、設備投資與改造、財務核算與...
模擬方法基本解釋 編輯 特點是可對已事過境遷的自然現象進行實驗研究,可將研究對象放大或縮小並在短時間內重複出現,可使人在某些特殊實驗中趨利避害。模擬方法英文...
《二級模擬題解基礎知識和FoxBASE程式設計》是2000年南開大學出版社出版的圖書,...第一部分 計算機基礎知識與基本操作 第1章 計算機系統的組成與套用 第2章 數制...
第2章 基本放大電路2.1 重點與難點學習輔導2.2 習題精解(全部習題)...械擬試題(3)參考文獻參考資料 1. 模擬電子技術基礎題解 .豆瓣讀書[引用日期...
第1章半導體的基本知識第2章半導體二極體及其電路第3章雙極型三極體及其放大電路第4章單極型場效應管及其放大電路第5章功率放大電路第6章集成運算放大電路...
書申明確了各章的知識要點和學習基本要求,針對每章教學內容提供了典型的例題分析方法。給出了各章自測題和習題的詳細解答。希望本書能使讀者掌握電子線路的基本概念...
2.1.1 放大電路的基本概念2.1.2 放大電路的組成原則模擬電子技術基礎習題解答適用對象 編輯 本書既可作為講授模擬電子技術課程教師的教師手冊,又可作為學生的輔導...
第二章 基本放大電路 一、例題(17) 例2.1 放大電路正常放大的判斷 例2.2 放大電路靜態工作點的計算 例2.3 PNP管單級放大電路靜態工作點計算 例2.4 微變等...
《學習指導與解題指南》是作者按照“高等工業學校電子技術基礎課程教學基本要求”,針對學生在學習中存在的問題和困難,結合多年的教學經驗編寫的。它是作者主編的《...
為便於讀者掌握課程的基本要求、重點和難點,書中精選了大量的例題與自我檢測題(附有解答)。書末附有典型的模擬電子技術基礎本科、專升本試卷和解答,以及碩士研究生...
電子技術課程教學指導小組制定的“電子技術基礎課程教學基本要求”和碩士學位研究生...並精選一些典型題進行了分析和評解,有解題思路和小結,每單元有精選習題並附有...
本書是根據前國家教委制定的高等工科院校模擬電子技術基礎的教學要求並結合目前的教改需要而編寫的輔導教材,其內容包括常用半導體器件、基本放大電路、多級放大電路、...
《電子信息?模擬電子技術基礎學習指導與習題全解》是作者參照“高等工業學校電子技術基礎課程教學基本要求”,結合作者多年的教學經驗編寫的。它是作者主編的《模擬電子...
本書聯繫實例編寫,並編排了大量的電路,使學生學習之後能基本了解模擬電子技術的工作過程和基本原理,並掌握模擬電子技術的基本技能。 [2] ...
