基本介紹
- 中文名：擬因子設計
- 所屬學科：數學
- 所屬問題：統計學（實驗設計）
- 相關概念：擬水平設計，正交表等
基本介紹,相關說明與距離舉例,
基本介紹
擬因子設計是指在水平數較少的正交表上安排某些水平數較多的因子的試驗的設計方法，多見於將三水平因子排入二水平正交表的情形。其作法是，由正交表的兩列(或若干列)組合成一個含較多水平的新列，將相應水平數的因子排入。例如，欲在正交表L8(27)(參見“正交表”)上安排一三水平因子，將其第2和第3列 作如下變換可以得到一個三水平的新列：
試驗號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
第2列第3列 | 11 | 11 | 22 | 22 | 12 | 12 | 21 | 21 |
新列 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 |
亦可利用其他對應關係構造新列，原則以重要水平重 複次數居多為佳。擬因子設計的試驗結果的統計分析有所改變：新列自由度較老列增加(仍為水平數減1)；一般平均和新列效應的估計量是有偏的，不過仍具有可比性；工程平均的估計量是無偏的。
相關說明與距離舉例
擬因子法的特點，在於能夠將水平數較多的因子排入水平數較少的正交表中，這對不是乘冪關係且相差不大的兩種水平比較實用。最常見的是把三水平因子排入二水平正交表中。
試考慮下列三個因子
其中A、C為二水平，B是三水平。如果要排入L8(27)表，則必須對正交表進行一定改造才行。
注意：A,C是二水平，在L8(27)表中其主效應各占一列，B是三水平，它的自由度
，應該在
表中占兩列。
先從 表中取出2列，例如2、3兩列。其同一橫行數對為(1，1)、(1，2)、(2，1)、(2，2)四種。
令 (1，1)為1 (1，2)為2
(2，1)為3 (2，2)為2
當然，對應關係的規定是任意的，一般將其認為重要的那個水平對應於兩種數對。這樣，2、3兩列便變成一個三水平列，可將因子B安排上去。由於2、3兩列的互動作用列是第一列，如果在這一列上安排一個二水平因子A，在第4列安排因子C，則為表2的設計。
A | B | C | 指標 | |
1 |  | 4 | ||
1 | 1 | 1 | 1 |  |
2 | 1 | 1 | 2 |  |
3 | 1 | 2 | 1 |  |
4 | 1 | 2 | 2 |  |
5 | 2 | 2 | 1 |  |
6 | 2 | 2 | 2 |  |
7 | 2 | 3 | 1 |  |
8 | 2 | 3 | 2 |  |
對這個設計，可用前四行A因子為A1時的考查指標比較B1與B2，用後四行A因子為A2時考查指標比較B2與B3。但是，這時B1和B3就不能直接比較，因為比較B1與B3的關係式
，既是B3與B1的平均差，又A2與A1一部分指標的平均差，這兩種平均差混雜在一起沒法區分。
看一看錶中B因子與C因子的關係，可以知道它們是不會發生上述問題的。根本原因在於第一列為原 表第二、三兩列的互動列，而第四列不是二、三兩列的互動列。因而我們得到一條經驗：在二水平正交表中，用某兩列構成一個三水平列後，該兩列的互動作用列不再適宜安排其他因子。
這樣，只得將因子A另作安排，原來的第一列就讓它閒著，叫它“賦閒”。這一列就稱為賦閒列。結果使 表被改造為下列形式；
安排 | 賦閒 | B | C | A | (B×A)1 | (B×A)2 |
列號 | 1 | | 4 | 5 | 6 | 7 |
安排好各個因子後，查 表的互動作用表，可以確定被改造為三水平的這個列與其他列的因子互動作用列表。由於三水平因子的互動作用應占兩列，它就是原 表的第二、三兩列分別與其他排有因子的列的互動作用列之和，如上表中B與A的互動作用列為第六與第七列。
用二水平正交表作擬因子設計，把任意兩列改造成一個新列後，這兩列的互動作用列必須“賦閒”。於是，在二水平正交表中，當安排二個以上的三水平因子作擬因子設計時，使改造後的幾個新列共有一個賦閒列，便可提高正交表的使用效率。
例如：
表的2、3列的互動列為1列，4、5列的互動列也是第一列，如果有兩個三水平因子時，對 表做擬因子設計，把2、3列與4、5列分別改造成兩個三水平列，這樣只賦閒一個列，即第一列。假如把2、3列改造為一個三水平列，再將4、8列改造為另一個三水平列，則必須將1列和12列同時“賦閒”，這種設計損失的效應列就多了。
擬因子設計後，各項效應計算略有不同，這要注意兩點。
1.未改造列的效應計算與正交表原來各列的效應計算一樣。
2.改造為多水平後的列的效應計算應有所校正。
比如前面 表作擬因子設計後，第一列賦閒，2、3列被改造為一個新的三水平列，可安排一個三水平因子，其他各列沒有改造。這時，三水平因子安排在改造了的新列中，它的三個水平效應分別計算為
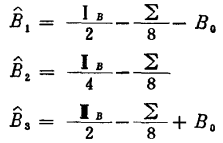
B0就是這個改造列的效應計算的校正項。
對於一般
正交表的擬因子設計，改造後的三水平列效應計算可用文字來表達。
如某擬因子設計，R是一個三水平因子，被安排在 表被改造的三水平列中，其R2水平試驗較R1和R3為多，它的各水平效應的計算是
校正項=
[R2對應於賦閒列的“1”水平的數據之平均值-R2對應於賦閒列的“2”水平的數據之平均值]。
