擬周期函式

擬周期函式(quasi-periodic function)是一種特殊的概周期函式，是周期函式的推廣，兩個周期函式疊加後不產生新的周期函式，這樣的函式叫做擬周期函式。“擬周期”概念的提出來自套用科學，比如在晶體理論和力學乃至混沌研究中都有套用。

基本介紹

• 中文名：擬周期函式
• 外文名：quasi-periodic function
• 所屬學科：數理科學
• 別名：殆周期函式
• 屬性：是周期函式的一種推廣
• 簡介：有某種近似周期性的有界連續函式
• 相關概念：周期函式，概周期函式等

基本介紹

擬周期函式(quasi-periodic function，也稱殆周期函式)，是周期函式的一種推廣，是具有某種近似周期性的有界連續函式。其數學描述如下：

對於函式，設有常數和C，使得

則稱為擬周期函式，L稱為函式的周期，C稱為函式相應於L的周期增量，或簡稱為周期增量。擬周期函式有無窮多個周期與周期增量。如果它有最小的正周期，則稱這個最小正周期為這個擬周期函式的主周期，相應的周期增量稱為主周期增量。

容易證明：

①周期函式是擬周期的；

②周期函式必是概周期的；

③擬周期函式必是概周期函式。

可見，擬周期函式是周期函式的推廣，是概周期函式的特殊情況。

相關性質

擬周期函式是在研究周期函式某種性質的基礎上進一步提出來的。三角多項式以及三角多項式序列的極限都是周期函式，而三角和

(其中，為複數，為實數)序列的極限卻未必是周期函式。但這類極限函式的特徵可以用某種近似周期性來刻畫。

考慮最簡單的情形，設和為連續周期函式，，設F為的周期，G為的周期。如果F和G是可公度的。即存在正整數和，使得，那么也為一周期函式，而且以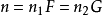為周期。但當F和G是不可公度時，雖然不存在整數和，滿足

但由有理數集的稠密性原理可知：存在正整數和，滿足，這裡，是事先任給的正數。從而存在數滿足和。

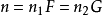
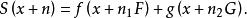
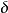
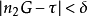
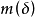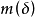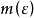還可以進一步證明更強的結論：對任給的，存在著正數，使得在每一個長為的區間內至少有一數滿足上式。這樣，由和的連續性、周期性以及上述事實便得到：對任給的存在著正數，使得在每一個長為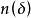的區間內至少有一數，滿足。

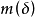
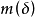
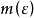
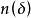
上式雖然並不能說明為周期函式，但它具有近似的周期性。一般來說，可以給出如下的精確描述：設為定義於實軸上的復值連續函式，如果滿足

就稱為的屬於的平移數。若對任意，存在，使得長度為的區間內至少包含一個的屬於的平移數，則稱為擬周期函式。

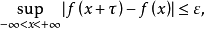
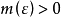
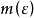
由上可知，任意有限個周期函式的和函式也必為擬周期函式。復值三角和必為擬周期函式。擬周期函式理論中的一個重要結果是：為擬周期函式若且唯若可以用上述的三角和序列來一致逼近。

由確定性微分方程描述的非線性動力學系統具有多種定態運動形式，其中平衡點、周期性(包括諧波、次諧波)、擬周期(或準周期)性、概周期和混沌運動等已為人們所認識。為了全面地揭示動力學系統的行為特徵，需要藉助於相空間和參數空問。上述運動形式在相空間中由其相應的軌線(例如分別由不動點、閉軌線、環面和奇異吸引子等)描述，在參數空間中，當系統參數在大範圍變化時，則由其相應的分支點(bifurcation point)、頻率捕捉區域(entrainment regions)表征。系統的相空間一般由其狀態變數構成，而參數空間則反映著一個系統所處的外部環境，它與外界的能量、信息和物質的交換都是通過其相應的參數實現的，所以對遠離平衡的耗散動力學系統而言，其參數空間是必不可少的。作為顯示系統中某個物理變數的具體方法，往往觀察其時間波形和功率譜的分布形式(分離或連續的)。物質總是以某種運動形式存在的，一個系統的整體行為特徵一般可通過某種變數反映出來，而且它的各種運動形式之間存在著內部聯繫。作為一種複雜的運動形式，混沌狀態的時間波形是非周期的，功率譜是寬頻連續的，軌線具有奇異吸引子結構。在一定條件下，通過調節適當的參數，系統可通過周期分支、擬周期運動等到達混沌。目前倍周期分支和切分支到達混沌的研究，已有大量的理論和實驗結果，關於擬周期運動及其向混沌的轉化在理論和數值模擬方面也有較多論證。作為介於周期與非周期之間的一種運動形式，擬周期狀態在動力學系統理論中並非新概念，然而要在物理實驗中正確識別並獲得這種狀態是困難的，也就是說，令人信服的物理實驗證實尚為數不多。

擬周期信號

擬周期信號(或波形)可表示為多種周期函式疊加的形式：

其中具有最小周期，頻率為，而且各個之間不可公度。另外，存在著一個有限的基本頻率集合，它具有這樣的性質：

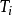
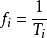
(1)它是線性獨立的，即不存在任何一個非零整數集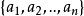，使得

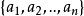
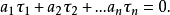
(2)它構成一個完全有限頻率基，總能找到某些非零整數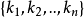，使得對於每個，有

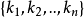
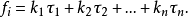
通常把具有n個基本頻率的擬周期信號稱做n-擬周期的。當然，當n=1時，擬周期信號就是一個周期波形。最簡單的2-擬周期波形為

其中的周期分別為，而且是互不公度的(incommensurable)。

一個常見的例子就是調相信號。如果m(t)的基本頻率為，則互不公度時，是具有基本頻率集合的2擬周期波形。