提升冪等元是環論的基本概念之一，指剩餘類環 R/𝔞 的冪等元轉化為 R 的冪等元。
基本介紹
- 中文名：提升冪等元
- 外文名：lifting idempotent element
- 適用範圍：數理科學
簡介,性質,剩餘類環,
簡介
提升冪等元是環論的基本概念之一，指剩餘類環 R/𝔞 的冪等元轉化為 R 的冪等元。
性質
設 𝔞 是 R 的理想，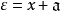
是 R/𝔞 的冪等元，若存在 R 的冪等元 e ，在自然同態 v 下有 v(e)=ε ，則稱 ε 提升到 e，若對 R/𝔞 到正交冪等元集
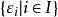，存在 R 的正交冪等元集 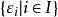，使得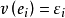
，則稱 R/𝔞 的正交冪等元集 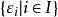可提升為 R 的正交冪等元集。
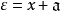
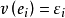
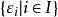
若 𝔞 是 R 的詣零理想，則 R/𝔞 的任意有限或可數正交冪等元集均可提升為 R 的正交冪等元集。若對 R 的每個理想 𝔞 而言， R/𝔞 的冪等元皆可提升為 R 的冪等元，則稱 R 為提升環，若 N 為 R 的一個根， R/N 的冪等元可提升為 R 的冪等元，則稱 R 對根 N 是提升的。
剩餘類環
(residue class ring)
剩餘類環是有理整數環的剩餘類環Z/mZ的推廣。設{F，S}為普通算術域，且F對S中每一賦值的剩餘類域均為有限域，設O為F的S整數環，A，B為O的理想，記N(A)=#(O/A)，稱為A的範數，它是積性的，O/A有許多類似於Z/mZ的性質：
1.bx≡c(mod A)有解若且唯若(b，A)除盡c，且模A/(b，A)解惟一(式中b，c，x∈O)；
2.以Φ(A)記環O/A中單位元個數，若(A，B)=1，則Φ(AB)=Φ(A)Φ(B)，且Φ(A)=N(A)∏(1-1/N(p))，式中p|A過素理想∑Φ(B)=N(A)，式中B|A過理想；
3.若b∈O，(b，A)=1，則bΦ(A)≡1(mod A)。
