振幅函式是關於任意多重指標的偏導數滿足某種類型不等式的函式,常取漸近展開的形式。
基本介紹
- 中文名:振幅函式
- 外文名:amplitude function
- 適用範圍:數理科學
簡介
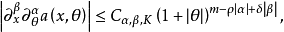
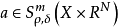
發展



振幅函式類

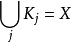
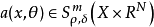
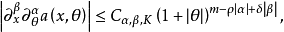
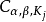
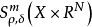
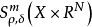
漸進展開形式
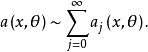
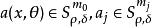
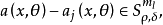
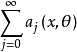
振幅函式是關於任意多重指標的偏導數滿足某種類型不等式的函式,常取漸近展開的形式。
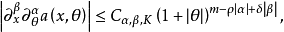
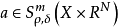




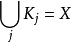
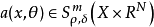
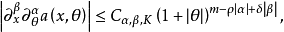
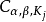
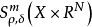
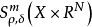
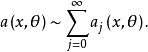
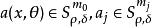
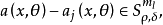
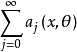
振幅函式是關於任意多重指標的偏導數滿足某種類型不等式的函式,常取漸近展開的形式。...
振幅是指振動的物理量可能達到的最大值,通常以A表示。它是表示振動的範圍和強度的物理量。
振幅調變也可簡稱為調幅,是在電子通信中使用的一種調製方法,最常用於無線電載波傳輸信息。在幅度調製中,載波的幅度(信號強度)是與所傳送的波形成比例變化的。例如...
1. 原子體系近核區電子波函式振幅 .國家圖書館[引用日期2014-07-25] V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:3次歷史版本 最近更新: 創建者:cvueifuj...
學科專業1 理論物理 學位級別 d 1994n 學位授予單位 中國科學技術大學 學位授予時間 1994 關鍵字 Penner模型 圈振幅 館藏號 O411 唯一標識符 108.ndlc.2.1...
所謂三角函式的通式,也就是三角函式的一般表達式。...... A:表示三角函式的振幅;三角函式的周期T=2π/ω;三角函式的頻率f=1/T:wx+t表示三角函式的相位;...
描述函式(describing function)一種表征元件特性的函式.是一種用一次諧波回響近似表征非線性元件特性的函式。...
英文名 airy function。英國英格蘭天文學家、數學家喬治·比德爾·艾里命名的特殊函式,他在1838年研究光學的時候遇到了這個函式。Ai(x)的記法是Harold Jeffreys引進...
振動物體離開平衡位置的最大距離叫振動的振幅。 振幅在數值上等於最大位移的大小。 振幅是標量,單位用米或厘米表示。振幅描述了物體振動幅度的大小又叫固有頻率(...
相應地,透射係數按餘弦或者正弦函式變化的光柵稱為正弦(振幅)光柵,如右圖所示。雙光束干涉圖樣的強度分布函式具有餘弦函式的形式,因此把一張記錄了雙光束干涉條紋的...
簡諧振動的圖像是正弦(餘弦)函式的圖像。...... 最簡的形式為f(x)=xsinx,它是偶函式,之所以能達到阻尼的效果,是因為y=x在定義域上單調,從而控制著sinx的振幅...
最大振幅比(largest amplitude ratio)窗函式最佳化的準則之一在給定窗函式頻譜主瓣寬度的條件下,其主瓣幅度與旁瓣最大幅度之比,稱為窗函式的振幅比。...
貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以19世紀德國天文學家F.W.貝塞爾的姓氏...
動態電路激勵作用下下,回響(輸出)相量與激勵(輸入)相量之比,稱為網路函式(network functions),記為H。在拉普拉斯變換下,將任意激勵表示為E(S),回響表示為D(S...
有限頻寬函式(bandlimited function)是一類特殊的函式。在頻譜空間中所有滿足|ξ|≤C的頻率ξ的集合稱為一個頻帶,頻譜位於這個頻帶的函式就稱為有限頻寬函式。確切...
正弦曲線或正弦波(Sinusoid/Sine wave)是一種來自數學三角函式中的正弦比例的曲線。也是模擬信號的代表,與代表數位訊號的方波相對。正弦曲線可表示為y=Asin(ωx+φ...
