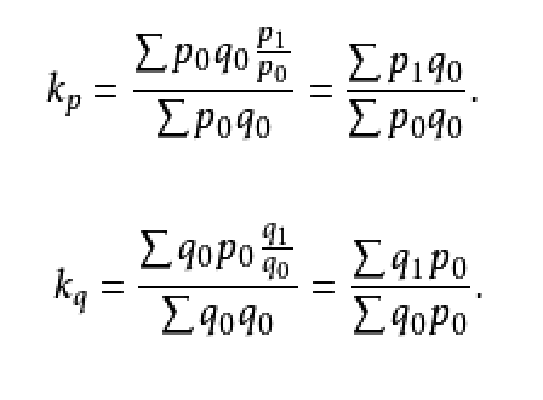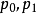拉氏公式

拉氏公式是1864年德國統計學家拉斯貝爾（Laspeyres）提出來的，又稱拉氏指數公式、拉斯貝爾指數公式，簡稱“拉式”或 “L式”，包括拉氏價格指數公式和拉氏物量指數公式。

基本介紹

• 中文名：拉氏公式
• 外文名：laspeyres' formula
• 別稱：拉氏指數公式、拉式、L式
• 所屬學科：數學（統計學）、經濟學
• 相關概念：拉氏指數，基期，報告期等

定義

拉氏公式又稱拉氏指數公式，簡稱“拉式”或 “L式”，由德國統計學家拉斯貝爾(Laspeyres，Ernst Louis Etienne，1834—1913)於1864年提出的一種指數公式。公式為：

拉氏價格指數公式：

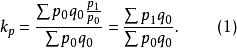
拉氏物量指數公式：

式中，分別為拉氏物價指數與拉氏物量指數；分別為商品基期的價格與報告期的價格；分別為商品基期的物量與報告期的物量。

拉氏指數

拉斯貝爾斯指數簡稱拉氏指數，是指用基期的銷售額作為權數，對個體價格指數求加權算術平均數，得出個綜合價格指數公式；同時，用基期銷售額(或產值)對個體物量指數求加權算術平均數，得出一個與價格綜合指數相對應的綜合物量指數的方法。這兩個指數都是德國人拉斯貝爾斯於1864年提出的。式（1）、（2）中的分別為拉氏物價指數與拉氏物量指數。

相關計算

拉氏指數公式可由三種加權取得。

1. 以加權的綜合式即得到拉氏式：

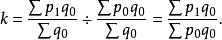
2. 以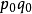加權的算術平均式，也可得到拉氏式：

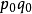
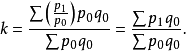
3.以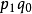加權的調和平均式，也可得到拉氏式：

例題分析

表1為某企業3種商品銷售量指數，試計算3種商品的銷售量綜合指數。

表1 3種商品銷售量指數計算表(萬元)

產品名稱	按基期價格計算		按報告期價格計算		銷售額變動
	基期銷售額p0q0	報告期銷售額p0q1	基期銷售額p1q0	報告期銷售額p1q1	p0q1-p0q0	p1q1-p1q0
甲	10	11.5	10	11.5	1.5	1.5
乙	10	11.0	11	12.1	1	1.1
丙	6	6.3	7.5	7.875	0.3	0.375
合計	26	28.8	28.5	31.475	2.8	2.975

解：根據拉氏公式和表1，可以得到某企業3種商品的銷售量綜合指數為

%.

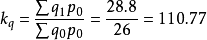
計算結果表明：3種商品銷售量總變動為報告期水平比基期水平增長了10.77%。同時，由於銷售量的增加而引起的銷售額的增加量為

（萬元）.