拉梅係數也稱拉梅常數。在正交曲線坐標系中,其坐標變數(u1,u2,u3)不一定都是長度,即不一定都是直角坐標系下的基坐標。可能是角度量,比如球面坐標和柱坐標體系中,很多坐標就是角度。其線元,必然有一個修正係數,這些修正係數稱為拉梅係數。
基本介紹
- 中文名:拉梅係數
- 外文名:Lame coefficient
- 發明人:G·拉梅
- 作用:數學研究
基本信息,創始人,
基本信息
比如
圓柱坐標系中的任意一點P沿r、φ和z方向的長度增量分別為
??dlr=dr, dlφ=rdφ, dlz=dz
則這裡拉梅係數就是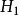 =1,
=1,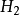 =r,
=r,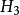 =1.
=1.
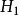
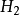
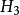
在球坐標系中H1=1,H2=r,H3=rsinθ
創始人
G·拉梅(Lame,Gabriel,1795.7.22-1870.5.1)法國數學家、工程師。生於法國的圖爾(Tours),卒於巴黎。1813年入巴黎綜合工科學校;1817年入巴黎礦業學院就學。1820年至1831年他在俄國的交通道路研究所工作。1829年成為彼得堡科學院通訊院士,1832年回到法國後,在巴黎綜合工科學校獲得教授職位。1843年成為巴黎科學院院士,1851年受聘為巴黎大學數學物理及機率論教授。
