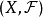投影極限

投影極限是通過一族拓撲線性空間定義的新的拓撲線性空間。在投影極限E上賦於關於族{(E_α,𝓛_α,u_α),a∈𝓐}的投影拓撲，稱為(E_α,u_αβ)的拓撲投影極限，或簡稱投影極限。

基本介紹

• 中文名：投影極限
• 外文名：projective limit
• 適用範圍：數理科學

簡介

局部凸空間的投影系

投影極限是通過一族拓撲線性空間定義的新的拓撲線性空間。

設(E_α,𝓛_α)(α∈𝓐)是一族分離局部凸空間，對任何β≥α定義了一個連續線性映射u_αβ:E_β→E_α如果滿足如下條件：

1.u_αα=I(α∈𝓐)；

2.u_αγ>=u_αβ° u_βγ(γ≥β≥a)，

則(E_α,u_αβ)稱為局部凸空間的投影系。

定義

做乘積空間是的子空間，它是由滿足下述條件的所有元素x= (x_α)組成，使得

則稱E為{E_α,a∈𝓐}關於映射u_αβ(α,β∈𝓐,β≥α)的投影極限，記為.或。

推廣

在投影極限E上賦於關於族{(E_α,𝓛_α,u_α),a∈𝓐}的投影拓撲，稱為(E_α,u_αβ)的拓撲投影極限，或簡稱投影極限，仍記為。

在一定意義下，投影極限和歸納極限這兩個概念是相互對偶的。

拓撲線性空間

設X為實數域或複數域K上的線性空間，是X上的拓撲，如果

（1）加法是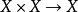的連續映射；

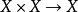
（2）數乘是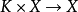的連續映射；

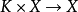
則稱是X上的向量拓撲或線性拓撲，稱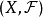為拓撲線性空間或拓撲向量空間。