基本介紹
- 中文名:截面二次軸矩
- 外文名:second axial moment of area
- 別稱:截面慣量
- 主條目:平行軸定理
簡介,定義,坐標變換,平行軸定理,轉軸公式,簡單截面的慣性矩,矩形截面,圓形截面,三角形截面,梁的彎曲正應力,與極慣性矩(截面二次極矩)的關係,
簡介
截面二次軸矩(second axial moment of area),又稱截面慣量,或截面對某一軸的慣性矩,通常是對受彎曲作用物體的橫截面而言,是反映截面的形狀與尺寸對彎曲變形影響的物理量。彎曲作用下的變形或撓度不僅取決於荷載的大小,還與橫截面的幾何特性有關。如工字梁的抗彎性能就比相同截面尺寸的矩形梁好。它和反映截面抗扭轉作用性能的極慣性矩是相似的。
截面二次軸矩雖然也稱“慣性矩”,但它和用以計算旋轉物體角加速度的慣性矩(常稱為轉動慣量)是不同的兩個概念。二者有相同的名稱,相同的符號I(I是英文中慣性 inertia 的首字母),但依據上下文二者不致混淆。而且二者的因次或單位不同:二次軸矩的因次是長度的四次方,而後者的因次是長度的二次方乘以質量。
定義
截面的面積為A,則
在國際單位制(SI)中,截面二次軸矩的單位是m^4,常用mm^4表示。
坐標變換
平行軸定理
主條目:平行軸定理
轉軸公式
下列公式可以計算坐標軸旋轉一個角度後截面對新坐標軸的慣性矩φ :旋轉的角度(逆時針) x = xcosφ + ysinφy = − xsinφ + ycosφIx 和 Iy :原坐標系下的慣性矩 Ix 和 Iy :坐標系轉動後新坐標系下的慣性矩。 公式
公式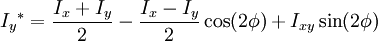 公式
公式
 公式
公式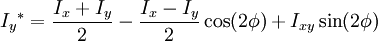 公式
公式簡單截面的慣性矩
矩形截面
b :寬度(x方向) h :高度(y方向)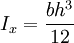 公式
公式 公式
公式
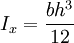 公式
公式 公式
公式圓形截面
D :直徑 r :半徑 公式
公式
 公式
公式三角形截面
以底邊方向為x方向
b :底邊寬度(x方向) h :高(y方向) 公式
公式
 公式
公式梁的彎曲正應力
由該式可見截面的慣性矩越大,彎曲正應力越小,抗彎性能越好。
與極慣性矩(截面二次極矩)的關係
由於ρ2 = y2 + z2,極慣性矩
IP = | ∫ | ρ2dA |
A |
根據截面二次軸矩的定義,可知:
IP = Iy + Iz
即截面對於任何一點的極慣性矩,等於該截面對以該點為原點的任意一組正交坐標系的截面二次軸矩之和
 公式
公式 公式
公式 公式
公式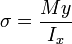 公式
公式