基本介紹
- 中文名:態疊加原理
- 外文名:principle of superposition of states
- 領域:量子力學
- 對象:微觀粒子粒子
- 實質:量子態的線性疊加
- 表現:微觀粒子的波粒二象性
定義



解釋



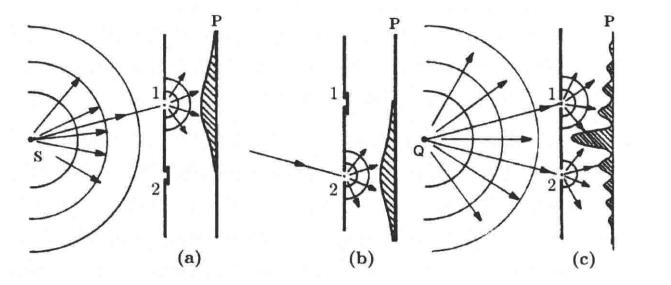 雙縫衍射實驗
雙縫衍射實驗
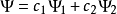

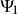





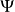


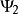


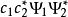




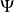






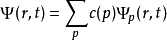







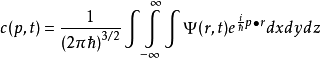

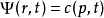


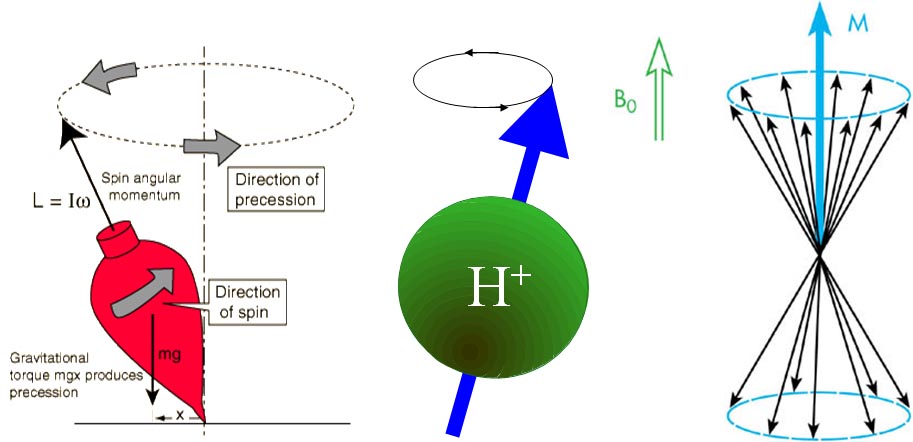






 雙縫衍射實驗
雙縫衍射實驗
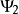
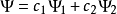

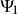





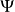


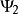


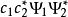




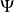
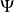


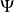




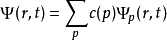







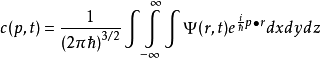

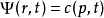


疊加態原理:疊加原理是量子力學中的一個基本原理, 廣泛套用於量子力學各個方面。態疊加原理實際上是在希爾伯特空間中構造一個形式上很像波函式的東西。...
疊加態,或稱疊加狀態(superposition state),是指一個量子系統的幾個量子態歸一化線性組合後得到的狀態。...
態矢量滿足線性,其對應的物理含義是態疊加原理。在定義內積後,可以選取正交完備的態矢量。一般而言,物理態所對應的態矢量是歸一的,這點對應於玻恩幾率詮釋。...
書中著重深入闡述態疊加原理,波函式的統計詮釋和不確定關係的物理內容及其本質意義,把他們看成是量子力學基本假設中所包含或者可以由此導出的結論。此外,書中還討論...
量子力學態疊加原理使得量子信息單元的狀態可以處於多種可能性的疊加狀態,從而導致量子信息處理從效率上相比於經典信息處理具有更大潛力。普通計算機中的2位暫存器在某...
根據態疊加原理,粒子的量子態,可以是幾個能量本徵函式的疊加。當測量粒子的能量時,測量的答案,只可能是疊加的幾個能級中的一個能級。由於測量會造成波函式坍縮,...
▪泡利不相容原理▪埃倫費斯特定理▪態疊加原理▪不確定性原理▪量子隧穿效應 ▪黑體輻射▪原子結構▪光電效應▪波粒二象性 ▪泡利不相容原理▪埃倫...
根據模態疊加原理,在已知各種載荷時間歷程的情況下,就可以預言結構物的實際振動的...(2)建立結構數學模型 根據已知條件,建立一種描述結構狀態及特性的模型,作為計算...
首先,將結構物在靜止狀態下進行人為激振,通過測量激振力與振動回響並進行雙通道...根據模態疊加原理,在已知各種載荷時間歷程的情況下,就可以預言結構物的實際振動的...
注意,這並不是指該系統只有兩個量子態,因為根據量子力學公設態疊加原理,系統可以處於這兩個獨立量子態的任意疊加態。若雙態系統中的二個量子態有相同的能量,則...
