愛爾可斯定理1:若△ABC和△DEF都是正三角形,則由線段AD、BE、CF的中心構成的三角形也是正三角形。 愛爾可斯定理2:若△ABC、△DEF、△GHI都是正三角形,則由三角形△ADG、△BEH、△CFI的重心構成的三角形是正三角形
基本介紹
- 中文名:愛爾可斯定理
- 外文名:Ai er ke si ding li
- 定理個數:2
- 定理套用範圍:求證正三角形
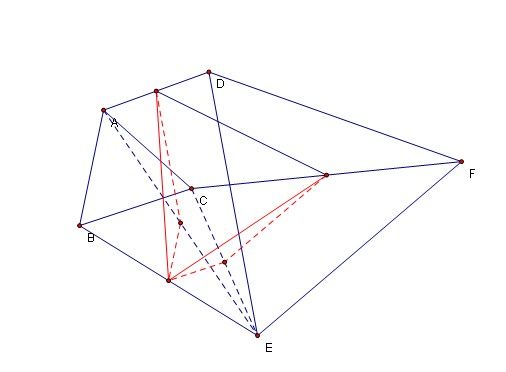
愛爾可斯定理1:若△ABC和△DEF都是正三角形,則由線段AD、BE、CF的中心構成的三角形也是正三角形。 愛爾可斯定理2:若△ABC、△DEF、△GHI都是正三角形,則由三角形△ADG、△BEH、△CFI的重心構成的三角形是正三角形
