基本介紹
- 中文名：心理力學
- 別稱：心理物理學
- 表達式：F=k(I2-I1)
- 提出者：孫雲飛
- 提出時間：2009年
- 套用學科：物理
- 適用領域範圍：心理學，社會學，經濟學，文學，人工智慧
心理力學的概述,介紹,力,功,衝量,力學群,力學群的概念,藝術群的概念,智慧型,介紹,運算元作用,
心理力學的概述
介紹
定義：運用力學來解釋心理需求。
解釋：心理力學主要將人的心理上的事情比作成了物體。心情所處的狀態比作物體的狀態。如果狀態差為負值，那么我們就認為是扭曲狀態，那么力就為斥力，而且人們心理上還會自發的差生將扭曲狀態變成正常狀態的吸引力，狀態下降，就會產生斥力，例如：一個很髒的屋子，人們會有將它弄乾淨的心理。如果屋子還處於髒的狀態沒有任何改變，那么等於沒有做功，如果狀態改變了，就是做功。
力
心理力學基本公式：
如果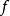
就是力，
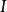屬於狀態，I2為末狀態或者需要，現狀，I1為原來狀態,k為常數，有下面公式
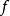
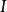
成立：
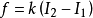
狀態上升，對自己會有引力，狀態下降，就會產生斥力，如果個體還有對手，那么個體狀態
心理力的性質：
對個體的吸引力，興趣主要在於方向||F||乘以||F(y)||小於F平均興趣水平。
有特定方向：力的對於一個體，所有吸引力全部指向自己。如同一個磁單極子一樣。
力的相對性：如果其他個體相對自己方向相同，相對自己引力。如果其他個體的力跟自己方向，就相 對自己為斥力。
力的多元性：力可以按性質分為很多類型，例如：美麗吸引力，尊敬吸引力，權威吸引力，規則吸引 力，未知吸引力，稀有吸引力，匹配吸引力，它們是線性無關的，也就是一個類型的力的變化不能決定另一個類型的力的變化。
力的合成：
例如：神奇就是未知吸引力跟稀有吸引力的組合。
功
功的概念：做功是力對狀態作用的效果。
物體對外做功就是放出能量。
功的性質：與路徑無關，跟狀態改變的差有關。
公式：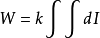 
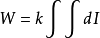
選擇也是做功
衝量
衝量公式：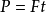
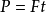
動量守恆：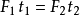
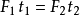
力學群
力學群是由代數學上的群論的內容，而且只具有群的部分功能，說法上仍然是群，只是為了更方便，更直觀，能夠清晰的述說一些複雜的力的性質跟結構。不同的吸引力對應不同的群，有些群具有對力的放大作用，有的群還有對力的改變的作用。
了解函式：對事情了解程度用
解釋。
力學群的概念
力學群是由同一類具有共同力學屬性的狀態或者力構成的群體，用x來解釋。力學群跟數學上的群不同在於不具有封閉性，主要套用了群的抽象功能，力學群是具有力產生主要在於元素某些結構具有，這些元素相同處在於可以用同一個用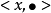
來訴說元素的性質跟結構，相互就構成了同構。
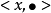
群的負群
稀有群：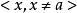
，a屬於平均值。
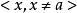
主流群：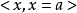
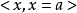
最優群：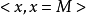
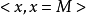
更優群：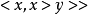
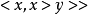
未知群：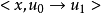
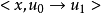
解釋群：
聚類群: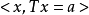 
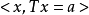
扭曲群：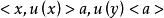
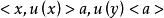
推理群：
距離群：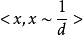
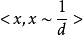
聚合群：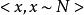
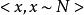
平庸群：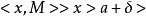
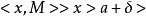
線性相關群：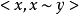
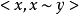
除此之外還有反射群，推理群，光環效應群。
藝術群的概念
具有藝術的性質的群，一般具有的力屬於引力，藝術有下列群：
密集群，對稱群，突變群，匹配群等。
用很小的戰勝很大的這個結構，利用的是扭曲跟稀有群跟未知群，也就是狀態小的通過神秘的過程最後反超過高的狀態的人，對於自己或者朋友，是吸引力。最後突出的勝利結果，負扭曲群且稀有群，不管什麼神秘過程，對於對手是斥力，斥力的人認為突出很神秘，認為用惡劣的手段成功，未知群且扭曲群。
智慧型
介紹
T運算元：對群進行改變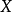
->
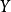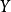,需要最需要狀態空間。
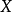
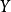
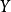
運算元公式：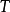
，.>
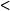
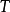
運算元作用
選擇，突出，截取，互補，對調，取代，改變群的結構，狀態，方向最後到對。如果追求高貴除外。
例子：對於處理某些突出線性無關部分，或者改變距離群的距離，改變大於變成小於，改變等於，最後到自己需求的。
