基本介紹
- 中文名：循環鍊表
- 外文名：cycle chain或circular linked list
- 分類：單循環，多重鏈
- 屬性：另一種形式的鏈式存貯結構
分類,空鏈判斷,尾指針,特點,
分類
循環鍊表（2）多重鏈的循環鍊表——將表中結點鏈在多個環上。
空鏈判斷
判斷空鍊表的條件是
head==head->next;
rear==rear->next;
尾指針
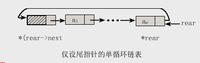
用尾指針rear表示的單循環鍊表對開始結點a1和終端結點an查找時間都是O(1)。而表的操作常常是在表的首尾位置上進行，因此，實用中多採用尾指針表示單循環鍊表。帶尾指針的單循環鍊表可見下圖。
注意：判斷空鍊表的條件為rear==rear->next;
特點
循環鍊表的特點是無須增加存儲量，僅對表的連結方式稍作改變，即可使得表處理更加方便靈活。
【例】在鍊表上實現將兩個線性表（a1，a2，…，an）和（b1，b2，…，bm）連線成一個線性表（a1，…，an，b1，…bm）的運算。
分析：若在單鍊表或頭指針表示的單循環表上做這種連結操作，都需要遍歷第一個鍊表，找到結點an，然後將結點b1鏈到an的後面，其執行時間是O(n)。若在尾指針表示的單循環鍊表上實現，則只需修改指針，無須遍歷，其執行時間是O(1)。
相應的算法如下：
LinkListConnect(LinkListA,LinkListB)
{//假設A，B為非空循環鍊表的尾指針
LinkListp=A->next;//①保存A表的頭結點位置
A->next=B->next->next;//②B表的開始結點連結到A表尾
free(B->next);//③釋放B表的頭結點
B->next=p;//④
returnB;//返回新循環鍊表的尾指針
}
注意：
①循環鍊表中沒有NULL指針。涉及遍歷操作時，其終止條件就不再是像非循環鍊表那樣判別p或p->next是否為空，而是判別它們是否等於某一指定指針，如頭指針或尾指針等。
②在單鍊表中，從一已知結點出發，只能訪問到該結點及其後續結點，無法找到該結點之前的其它結點。而在單循環鍊表中，從任一結點出發都可訪問到表中所有結點，這一優點使某些運算在單循環鍊表上易於實現。
/* 設立尾指針的單循環鍊表的12個基本操作 */
void InitList(LinkList *L) {
/* 操作結果：構造一個空的線性表L */
*L=(LinkList)malloc(sizeof(struct LNode));
/* 產生頭結點，並使L指向此頭結點 */
if(!*L) /* 存儲分配失敗 */
exit(OVERFLOW);
(*L)->next=*L;
/* 指針域指向頭結點 */
}
void DestroyList(LinkList *L) {
/* 操作結果：銷毀線性表L */
LinkList q,p=(*L)->next;
/* p指向頭結點 */
while(p!=*L) { /* 沒到表尾 */
q=p->next;
free(p);
p=q;
}
free(*L);
*L=NULL;
}
void ClearList(LinkList *L)
/* 改變L */
{
/* 初始條件：線性表L已存在。操作結果：將L重置為空表 */
LinkList p,q;
*L=(*L)->next;
/* L指向頭結點 */
p=(*L)->next;
/* p指向第一個結點 */
while(p!=*L)
/* 沒到表尾 */
{
q=p->next;
free(p);
p=q;
}
(*L)->next=*L;
/* 頭結點指針域指向自身 */
}
Status ListEmpty(LinkList L) {
/* 初始條件：線性表L已存在。操作結果：若L為空表，則返回TRUE，否則返回FALSE */
if(L->next==L)
/* 空 */
return TRUE;
else
return FALSE;
}
int ListLength(LinkList L) {
/* 初始條件：L已存在。操作結果：返回L中數據元素個數 */
int i=0;
LinkList p=L->next;
/* p指向頭結點 */
while(p!=L)
/* 沒到表尾 */
{
i++;
p=p->next;
}
return i;
}
Status GetElem(LinkList L,int i,ElemType *e) {
/* 當第i個元素存在時，其值賦給e並返回OK，否則返回ERROR */
int j=1;
/* 初始化，j為計數器 */
LinkList p=L->next->next;
/* p指向第一個結點 */
if(i<=0||i>ListLength(L))
/* 第i個元素不存在 */
return ERROR;
while(j< i) {
/* 順指針向後查找，直到p指向第i個元素 */
p=p->next;
j++;
}
*e=p->data; /* 取第i個元素 */ return OK;
}
int LocateElem(LinkList L,ElemType e,Status(*compare)(ElemType,ElemType)) {
/* 初始條件：線性表L已存在，compare()是數據元素判定函式 */ /* 操作結果：返回L中第1個與e滿足關係compare()的數據元素的位序。*/ /*若這樣的數據元素不存在，則返回值為0 */ int i=0;
LinkList p=L->next->next; /* p指向第一個結點 */ while(p!=L->next) {
i++;
if(compare(p->data,e)) /* 滿足關係 */
return i;
p=p->next;
}
return 0;
}
Status PriorElem(LinkList L,ElemType cur_e,ElemType *pre_e) {
/* 初始條件：線性表L已存在 */ /* 操作結果：若cur_e是L的數據元素，且不是第一個，則用pre_e返回它的前驅，*/ /*否則操作失敗，pre_e無定義 */ LinkList q,p=L->next->next; /* p指向第一個結點 */ q=p->next;
while(q!=L->next) { /* p沒到表尾 */
if(q->data==cur_e) {
*pre_e=p->data;
return TRUE;
}
p=q;
q=q->next;
}
return FALSE; /* 操作失敗 */
}
Status NextElem(LinkList L,ElemType cur_e,ElemType *next_e) {
/* 初始條件：線性表L已存在 */ /* 操作結果：若cur_e是L的數據元素，且不是最後一個，則用next_e返回它的後繼，*/ /*否則操作失敗，next_e無定義 */ LinkList p=L->next->next; /* p指向第一個結點 */ while(p!=L) { /* p沒到表尾 */
if(p->data==cur_e) {
*next_e=p->next->data;
return TRUE;
}
p=p->next;
}
return FALSE; /* 操作失敗 */
}
Status ListInsert(LinkList *L,int i,ElemType e) { /* 改變L */
/* 在L的第i個位置之前插入元素e */ LinkList p=(*L)->next,s; /* p指向頭結點 */ int j=0;
if(i<=0||i>ListLength(*L)+1) /* 無法在第i個元素之前插入 */
return ERROR;
while(j< i-1) { /* 尋找第i-1個結點 */
p=p->next;
j++;
}
s=(LinkList)malloc(sizeof(struct LNode)); /* 生成新結點 */ s->data=e; /* 插入L中 */ s->next=p->next;
p->next=s;
if(p==*L) /* 改變尾結點 */
*L=s;
return OK;
}
Status ListDelete(LinkList *L,int i,ElemType *e) { /* 改變L */
/* 刪除L的第i個元素，並由e返回其值 */ LinkList p=(*L)->next,q; /* p指向頭結點 */ int j=0;
if(i<=0||i>ListLength(*L)) /* 第i個元素不存在 */
return ERROR;
while(j< i-1) { /* 尋找第i-1個結點 */
p=p->next;
j++;
}
q=p->next; /* q指向待刪除結點 */ p->next=q->next;
*e=q->data;
if(*L==q) /* 刪除的是表尾元素 */
*L=p;
free(q); /* 釋放待刪除結點 */ return OK;
}
void ListTraverse(LinkList L,void(*vi)(ElemType)) {
/* 初始條件：L已存在。操作結果：依次對L的每個數據元素調用函式vi() */ LinkList p=L->next->next; /* p指向首元結點 */ while(p!=L->next) { /* p不指向頭結點 */
vi(p->data);
p=p->next;
}
printf("\n");
}
