一無源支路兩端的電壓與其中的電流的比值稱為該支路的復阻抗,單位為歐(Ω)。它是反映一段無源電路或無源二端網路電性質的物理量。在交流電路的複數解法中,把電壓電流等簡諧量都用其對應複數表示,分別稱為復電壓、復電流,因此電壓和電流的比值也同為複數,稱之為復阻抗。
基本介紹
- 中文名:復阻抗
- 外文名:Complex Impedance
- 定義:無源支路兩端的電壓與電流的比值
- 公式:Z=U/Iej(z-i)=zejφ
定義
復阻抗的模——阻抗

復阻抗的幅角——阻抗角
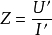
RLC串聯電路的復阻抗
RLC串聯電路
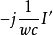
一無源支路兩端的電壓與其中的電流的比值稱為該支路的復阻抗,單位為歐(Ω)。它是反映一段無源電路或無源二端網路電性質的物理量。在交流電路的複數解法中,把電壓電流等簡諧量都用其對應複數表示,分別稱為復電壓、復電流,因此電壓和電流的比值也同為複數,稱之為復阻抗。

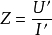
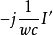
一無源支路兩端的電壓與其中的電流的比值稱為該支路的復阻抗,單位為歐(Ω)。它是反映一段無源電路或無源二端網路電性質的物理量。在交流電路的複數解法中,把電壓...
阻抗圓圖是指利用歸一化阻抗與反射係數之間的一一對應關係,將歸一化阻抗表示在反射係數復平面上(包括兩個曲線坐標系統:反射係數曲線坐標、歸一化阻抗曲線坐標和四簇...
它的倒數定義為該網路的入端複數導納,簡稱導納,分別用符號Z和Y表示。複數阻抗的實部稱為等效電阻,虛部稱為電抗,模稱為阻抗模,幅角稱為阻抗角,它們分別用符號R...
2 復阻抗 ▪ 示性函式 ▪ 正弦穩定狀態 3 串聯 ▪ 電流 ▪ 傳遞函式 ▪ 增益和相位 ▪ 相量表示 ▪ 脈衝回響 ▪ 零輸入回響 RL...
由於電容復阻抗和容值成反比,所以電容的串並聯和電阻的算法正好相反。擬電容器放電過程 編輯 加在電容器兩個極板上的交流電頻率高,電容器的充放電次數增多;充放電...
5.5 復阻抗運算 (91)5.5.1 復阻抗的串聯 (91)5.5.2 復阻抗的並聯 (92)5.5.3 復阻抗與復導納的轉換 (93)5.6 無源單口網路中的功率 (93)...
4.6.2 復阻抗與復導納的等效變換 874.7 RLC串聯電路 894.7.1 電壓與電流的關係 894.7.2 電路的性質 894.7.3 阻抗串聯電路 90...
與渦流伴生的感應磁場與原磁場疊加,使得檢測線圈的復阻抗發生變化。導體內感生渦流的幅值、相位、流動形式及其伴生磁場受導體的物理特性影響,因此通過監測檢測線圈的阻...
一、復阻抗二、復導納7.6用相量法求解電路的正弦穩態回響一、正弦穩態分析方法之一——等效變換法二、正弦穩態分析方法之二——電路方程法...
4.4 串並聯電路的諧振4.4.1 復阻抗的頻率特性4.4.2 諧振頻率的計算本章小結思考與練習題4第5章 三相電路5.1 三相電路5.1.1 三相電源5.1.2 三相電路...
