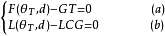復原力臂（righting arm）是指復原力矩所對應的力臂，復原力矩是船舶受外力作用傾斜時由於重力和浮力的作用點不在同一鉛垂線上所產生的使船恢復正態的力矩。
基本介紹
- 中文名：復原力臂
- 外文名：righting arm
- 定義：復原力矩所對應的力臂
- 相關：復原力矩
- 一級學科：船舶工程
- 二級學科：船舶總體
最大復原力臂,復原力矩,復原力臂計算原理,
最大復原力臂
最大復原力臂（見圖1）是復原力矩最大時對應的力臂。此時船舶的穩性力矩最大，抵抗外界力矩作用最大的時候。此時船舶傾斜的角度稱之為極限靜傾角。
圖1
圖1船舶受到外力矩作用會產生橫傾。此時船舶的穩性（本身穩性指的就是使船舶恢復自身原先穩定狀態的能力）力矩就會開始作用來抵抗這個外力矩，穩性力矩的作用就是想使船舶恢復原先穩定的狀態。因此把穩性力矩又稱作復原力矩，即使船舶恢復原來狀態的力矩。
復原力矩
復原力矩是船舶受外力作用傾斜時由於重力和浮力的作用點不在同一鉛垂線上所產生的使船恢復正態的力矩。以橫傾為例，如圖2所示。漂浮於水線W1L1的船繞縱向水平軸橫傾至水線W2L2，重心和浮心不在同一垂線上，重力和浮力形成力偶，促使船回到初始平衡位置，此時的復原力矩為正值。當重力和浮力形成的力偶，促使船繼續橫傾，此時的復原力矩為負值。復原力矩是排水量與重心G至浮力作用線的垂直距離GZ的乘積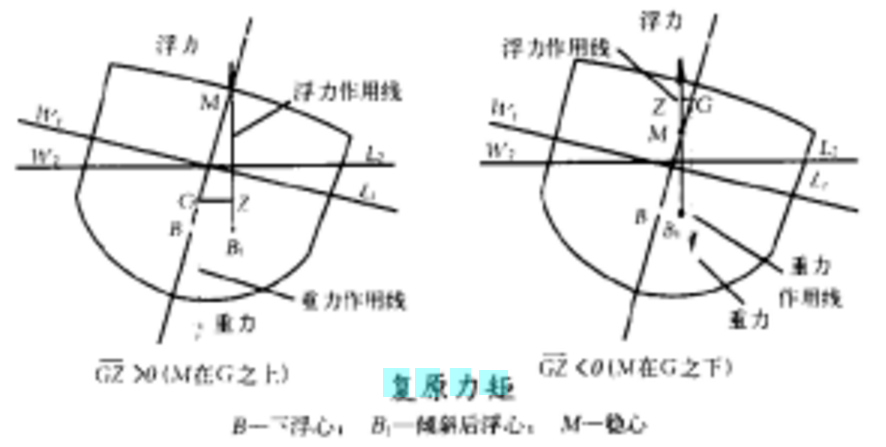
圖2
圖2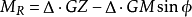
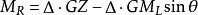
式中MR為復原力矩，△為排水量，GZ為復原力臂，GM為初重穩距，GML為初縱重穩距，
為橫傾角，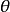
為縱傾角。復原力矩或復原力臂是船舶穩性的重要特徵數之一。在靜穩性中，當船舶橫傾至某一角度時的復原力矩等於傾斜力矩時，船平衡於該傾角。在動穩性中，當船的復原力矩所作的功與傾斜力矩所作的功相等時，橫傾角速度消失。
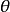
復原力臂計算原理
穩性計算的關鍵問題是計算靜穩性曲線，靜穩性計算的基礎是復原力臂的計算。自由浮態下復原力臂計算的關鍵問題是，當浮體在外力矩作用下產生橫傾角
時，計算吃水d和縱傾角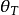
，使得浮力等於重力，浮心縱向位置等於重心縱向位置。該問題可以簡化為如下數學模型：
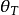
式(a)為浮力平衡方程（浮力等於重力），其中
，其中ρ為海水密度，V為對應浮態下的排水體積；式(b)為縱向力矩平衡方程，其中L(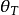，d)=LCB，其中LCB為對應浮態下的浮心縱向位置。
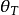
復原力臂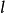
為橫傾角的函式，即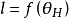
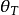。當在外力矩作用下浮體產生的橫傾角為時，通過求解上述方程得到d和，然後通過計算浮心與重心之間的距離確定對應橫傾角下的復原力臂。
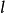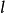
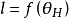
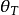
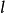
上述方程有兩個方程和兩個未知數，理論上有唯一解。但是由於浮式海洋結構物浮體幾何形狀的複雜性，浮力和浮心位置沒有解析表達式，因而該方程也無解析解。採用常規的最佳化方法求解，存在運算量太大而且有時會出現不收斂等問題。因而介紹一種基於三維浮體模型的復原力臂通用疊代求解算法。
求解自由浮態下的復原力臂流程如圖3所示，具體步驟如下：
圖3
圖3(1)通過靜水力公式計算當前吃水d0，作為疊代的初始值。設定重力與浮力差的精度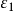
和重心與浮心距離差的精度
。
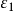
(2)通過實體的旋轉變換，使B- Rep浮體模型產生橫傾。
(3)固定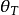，搜尋d使得浮力平衡方程在設定的精度下成立。
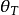
(4)在設定精度下，判斷此時的力矩平衡方程是否成立，若成立則執行步驟(7)，否則執行步驟(5)。
(5)固定d，搜尋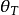使得力矩平衡方程在設定的精度下成立。
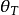
(6)在設定精度下，判斷此時的浮力平衡方程是否成立，若成立則執行步驟(7)，否則執行步驟(3)。
(7)疊代求解結束，此時浮心與重心之間的垂直距離即為自由液面修正前的復原力臂
。
通過三維艙室實體模型，計算此時自由液面的修正力臂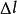
，則對應的復原力臂為
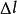
(8)完成基於B- Rep浮體模型的自由浮態下復原力臂計算。
採用上述復原力臂計算方法，計算不同橫傾角下的復原力臂，並以橫傾角為橫坐標，對應橫傾角下復原力臂為縱坐標繪製曲線，則該曲線就是自由浮態下的靜穩性曲線。通過上述算法，可以完成船舶、海洋平台和其他海洋結構物的自由浮態下的穩性計算。
