概念
 影響線(圖1)
影響線(圖1)橋樑上行駛的火車、汽車,活動的人群,吊車樑上行駛的吊車等等,這類作用位置經常變動的荷載稱為移動荷載。常見的移動荷載有:間距保持不變的幾個集中力(稱為
行列荷載)和
均布荷載。為了簡化問題,我們往往先從單個移動荷載的分析入手,再根據
疊加原理來分析多個荷載以及均布荷載作用的情形。
對於工程計算中的各種物理量和
幾何量,我們,記作Z。
由於移動荷載的作用位置是變化的,使得結構的支座反力、截面
內力、應力、變形等等也是變化的。因此,在移動荷載作用下,我們不僅要了解結構不同部位處量值的變化規律,還要了解結構同一點處的量值隨荷載位置變化而變化的規律,以便找出可能發生的最大內力是多少,發生的位置在哪裡,此時荷載位置又怎樣,從而保證結構的安全設計和施工。在豎向單位移動荷載作用下,結構內力、反力或變形的量值隨豎向單位荷載位置移動而變化的規律圖像稱為影響線。
影響線表示結構中由沿結構跨度移動的單位載荷引起的內力、位移或反力等的數值(稱影響值)隨單位載荷作用位置變化的曲線,它可用於確定在多種載荷共同作用下的影響值,也可用於確定結構上移動載荷的最不利位置。
在工程中,影響線描繪了沿著沿著結構任意點放置的單位負載引起的梁或桁架上特定點處功能變化(如結構構件中的剪下氈)影響線研究的一些常用功能包括反應(結構支撐必須施加的力以使結構保持靜止)、
剪下力、
力矩和
撓度。影響線在設計用於橋樑、起重機軌道、輸送帶、地板梁和其他負載將沿其跨度移動的其他結構中的梁和桁架是重要的。影響線顯示負載將為所研究的任何功能產生最大效果。
影響線使用標量和加法。這意味著即使施加的負載不是單位負載或者施加多個負載,也可以使用它們。為了發現任何非單位負載對結構的影響,由影響線獲得的縱坐標結果乘以要施加的實際負載的大小。整個影響線可以被縮放,或者只是沿線的最大和最小效果。縮放的最大和最小值是必須在梁或桁架中設計的臨界大小。
在多個負載可能有效的情況下,可以將各個負載的影響線相加在一起,以獲得結構在給定點處感覺到的總效應。當將影響線一起添加時,由於跨越結構的負載間隔,必須包括適當的偏移量。例如,卡車負載被施加到結構。後橋B,在前橋A後面三英尺處,則沿結構的x腳處的A的作用必須加在B的(x-3)腳沿結構的作用上,而不是B的作用沿著結構的x腳。
許多負載分布而不是集中的。影響線可以用於集中或分散式負載。對於集中(或點)負載,單位點負載沿結構移動。對於給定寬度的分布載荷,沿著結構移動相同寬度的單位分布載荷,注意到當載荷接近端部並離開結構時,只有部分總載荷由結構承載。分散式單位負荷的影響也可以通過將點負荷的影響線整合到相應的結構長度上來獲得。
舉例
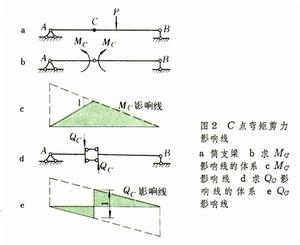 影響線(圖2)
影響線(圖2)伸臂梁的影響線內力影響線的
量綱影響線與
內力圖的區別影響線繪製舉例
跨中截面是指兩支座間的截面。在不動荷載作用下求這種截面內力時要先求支座反力,然後通過支座反力求內力。作影響線時也是這樣,先繪支座反力的影響線,然後通過它,繪內力影響線。
(2)伸臂梁挑臂截面內力影響線
求挑臂上內力與求懸臂樑上內力一樣,無需先求支座反力,取自由端一側作為截離體。求內力影響線時也是這樣。
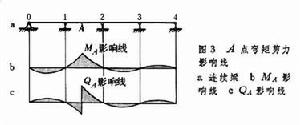 影響線(圖3)
影響線(圖3)由於任何值(支座反力、
剪力、
彎矩等)影響線的縱標均代表移動單位力P=I所產生的該量值的值,而P=I
無量綱,所以該量值影響線縱標的
量綱為該量值的量綱與力的量綱的比值。彎矩影響線的量綱為(長度單位)剪力、支座反力影響線的量綱即為
無名數。
內力圖(M、Q、N圖)是表示各個截面內力值的圖。它所對應的荷載位置是不變的。內力圖橫標代表截面位置,縱標代表不同截面內力之值。
影響線是表示P=1移動時指定截面內力值變化的圖。這裡是截面位置是不變的。橫標代表P=1的位置,縱標代表p=1在不同位置上時相應截面的內力值。
計算
下圖表示一
簡支梁和簡支梁
A端反力
RA的影響線。圖中橫坐標
x表示單位載荷(P=1)的作用位置,縱坐標
y表示
RA的值。圖中表示出
RA隨單位載荷作用位置的變化規律。
簡支梁和A端反力的影響線
若一個數值為P0的載荷作用在樑上x處,而影響線上與x對應的影響值為y,則實際影響值的大小為P0y;若一組載荷P1,P2,…,Pn作用在樑上,它們的作用位置分別為x1x2,…,xn,並且影響線上的影響值分別為y1,y2,…,yn,則P1,P2,…,Pn共同作用下的影響值為
影響線的這種用法可推廣到一般結構。
利用某量值S(某支座反力、某截面
彎矩、
剪力等)的影響線,求位置一定的一組荷載產生的該量值S之值(叫S的
影響量)。
作用在影響線同一直線線段上的各力的影響等於其合力的影響,即
其成立的條件是各力位於S影響線的同一直線線段上。據此,不能將S影響線頂點B兩側之力以一個合力代替去計算S。
均布荷載產生的
影響量S等於荷載
集度口與荷載下面的S影響線的面積的乘積。注意:均布荷載下面的影響線縱標有正有負,因此,面積也有正有負,這個結論,對於曲線型影響線(如靜不定力影響線)也是成立的。對於位於影響線同一直線段上的分布荷載也可用其合力代替去求影響量。
影響方程
在思路上與
靜定結構內力影響線一樣一是建立影響方程;二是建立影響方程的方法,與固定荷載作用下求內力的方法相同。即靜 定結構用
平衡方程建立影響方程,而
超靜定結構則用解超靜定的方法——力法、
位移法、力矩分配法等建立影響方程。
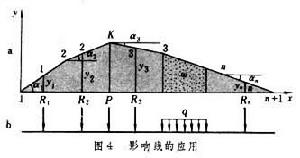 影響線(圖4)
影響線(圖4)根據影響方程來繪製影響線的方法叫靜力法。用繪製位移圖的方法來得到影響線的方法叫機動法。機動法有一個很大的優點,就 是能很快地畫出內力影響線的形狀,以判定荷載的最不利分布,而這是計算最大內力值所需要的。
①欲繪製超靜定結構支座反力R的影響線,則去掉相應聯繫(支桿),把支桿反力R暴露出來,沿反力R正向加一個力使與之相應的 廣義位移(豎向位移)等於1,這樣得到的位移圖(撓度曲線)即為R的影響線。符號:軸線上面的縱標取正號。
②欲繪製
超靜定結構彎矩MK影響線形狀,應把截面K切斷,再用鉸聯結起來(把剛結變為鉸結,丟掉了阻止相對轉動的聯繫)。沿 彎矩正向(使下面受拉)加一對大小任意的
力偶矩M。畫出位移圖的形狀,軸線上方取為正,這就得到了影響線的形狀。
③欲繪製超靜定結構
剪力影響線形狀,應把截面K切斷,再用一對平行桿聯結起來(去掉了阻止相對錯動的聯繫)。採用這種方式 時,左右兩部分只能相對錯動,而不能相對轉動(和沿軸向相對移動),因之體系變形後,左右兩部分變形曲線於聯結處的切線相互平行。沿 剪力正向加一對任意大小的剪力Q畫出位移圖,即得影響線的形狀。上面取正號,下面取負號。
由於
超靜定結構去掉一個聯繫後仍為一
幾何不變體系,其位移圖是曲線的,所以超靜定結構內力的影響線是曲線的。由於靜定結 構去掉一個聯繫後即成為機構(可變體系),其位移圖是直線圖形,因而
靜定結構內力影響線是直線圖形。超靜定結構中的靜定內力(如挑臂 上的
彎矩、
剪力),其影響線也是直線圖形。
影響形狀
①對於跨中載面,當活荷載作用於載面所在跨及每間隔一跨的各跨上時,出現最大
正彎矩。
②對於支座截面,當活荷載作用於該支座左右兩跨及每間隔一跨的各跨上時,出現最大
負彎矩。
③在整個結構上都布滿活荷載時,對於支座
彎矩、跨中彎矩都不是最不利情況。
④一種內力出現最大(最小)值時,其他內力並不同時出現最大(最小)值。
與活荷載不同,恆荷載經常作用,永遠要計算,沒有最不利分布問題。
確定
(1)有一個集中力居於影響線頂點上。
(2)將行列荷載自此左移一點,(圖3)是正的,右移一點(圖4)是負的。滿足這種條件(使取得極大值)的位於影響線頂點上的集中力叫臨界荷 載(以表示),與此對應的行列荷載位置,稱為臨界位置。
 圖3
圖3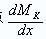 圖4
圖4(3)MK在行列荷載移動全過程中得到的極大值可能不止一個。
對於三角形影響線:多邊形影響線,在由多個集中力組成的行列荷載作用下,都是適用的。S生極大值所對應的行列荷載位置,必 須具備以下兩個條件:
①有一個集中力位於影響線的頂點上。
②自此位置向左移:自此位置向右移:。這兩個公式稱為臨界條件,滿足臨界條件的集中力為臨界荷載,相應的荷載位置為臨界 位置。
把臨界荷載算在影響線頂點的哪一邊,哪一邊單位長度上的平均荷載就大。
對於三角形影響線,求量值S最大值的步驟為:
①按前述方法估計能產生最大值的若干可能的臨界荷載。
②逐個地把估出的力放在影響線頂點上,驗算是否滿足臨界條件。
如果滿足臨界條件,則利用影響線求出相應的S,它是S一個
極大值。比較這樣求得的幾個S極大值,其中最大的就是行列荷載移劫 過程中可能產生的最大S值。
根據臨界條件的推導過程知:臨界條件中的前一個不等式代表力在左方時後一個不等式代表力在右方時。若滿足前一個不等式, 而不滿足後一個不等式,就表明不論把力放在左面,還是放在右面,都有即越往右移S越大。因此應把行列荷載向右移。反之,若不滿足前一個 不等式,而滿足後一個不等式,則不論力在左、力在右都有即越往右移S越小,因此求S極大值耍向左移動
行列荷載。對於橋樑要考慮車輛右行 ,左行兩種情況,按最不利情況設計。工業廠房
吊車荷載則不會改變方向。
 影響線(圖1)
影響線(圖1) 影響線(圖2)
影響線(圖2) 影響線(圖3)
影響線(圖3)



 影響線(圖4)
影響線(圖4) 圖3
圖3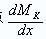 圖4
圖4