彈性穩定性的本徵問題

在用線彈性小撓度理論求彈性結構失穩臨界載荷時，可通過如下數學推導，把穩定性問題最後歸結為一種特殊形式的齊次線性代數方程組的本徵值問題。

基本介紹

• 中文名：彈性穩定性的本徵問題
• 外文名：eigenvalueproblem of elastic stability
• 類型：物理類
• 隸屬：彈性系統

設彈性物體在一組廣義力Q₁，Q₂，…，Q_n作用下，產生相應的廣義位移q₁，q₂，…，q_n，並處於平衡狀態，則彈性物體的總勢能可表示為廣義位移的函式，即=（q₁，q₂，…，q_n）。

總勢能的一次變分為：

相當於彈性物體的平衡條件。在平衡狀態下，總勢能的二次變分為：

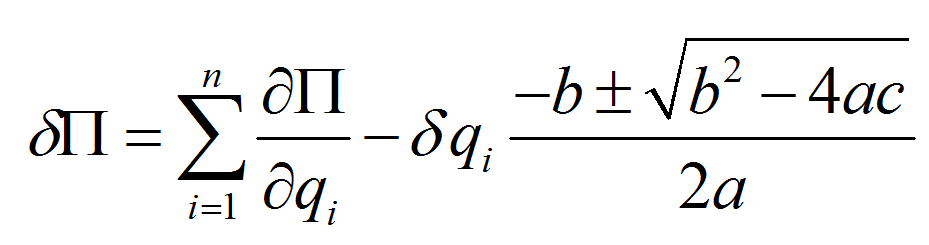
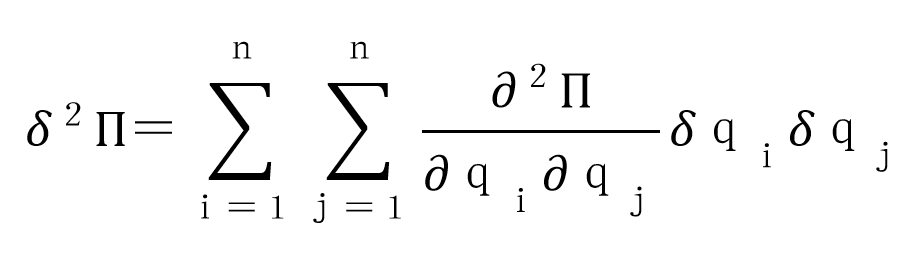
用矩陣形式可表為：

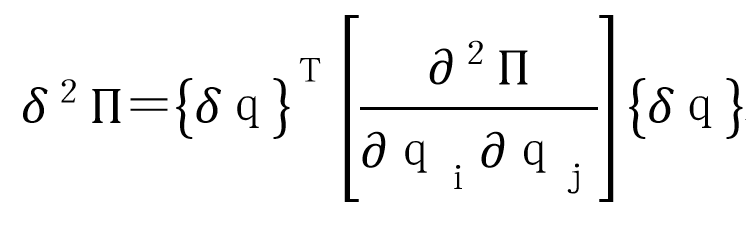
式中為由廣義坐標的變分組成的陣列；上標“T”表示矩陣的轉置；二次變分有三種可能情況：若所有都使>0，則平衡是穩定的；若有某一個能使<0，則平衡是不穩定的，若某一個或幾個能使=0，其餘使>0，則平衡是隨遇的。

矩陣可表為下列兩矩陣之差：

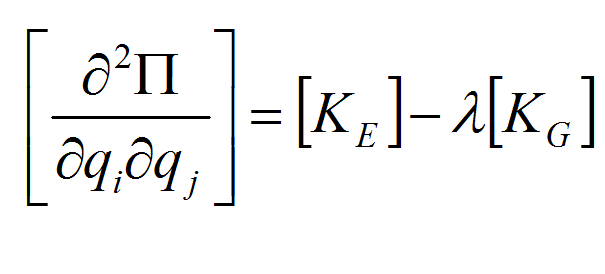
式中[K_E]為結構的彈性剛度矩陣；[K_G]為結構的幾何剛度矩陣，為與載荷有關的參數。

由隨遇平衡條件=0可得到：

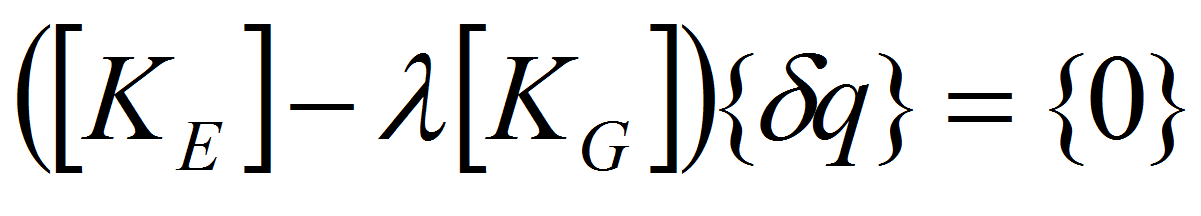
用這一類式子所表示的問題為齊次線性代數方程組的本徵值問題，為本徵值（又稱特徵值）。通過線性代數的方法和數值方法可求出，進而可求得失穩臨界載荷。例如彈性桿承受一軸向壓力N和其他廣義力，在這種情況下，為軸向壓力的失穩臨界值N_cr和初加軸向壓力N之比。求出後，再由N_cr=拉姆達N便可求出N_cr。