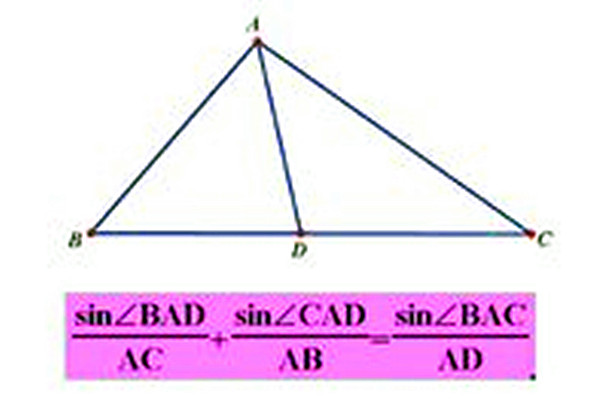
張角定理，指的是在△ABC中，D是BC上的一點，連結AD。那么sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD。
基本介紹
- 中文名：張角定理
- 外文名：Spread Angle theorem
- 表達式：sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD
- 提出者：朱謙
- 提出時間：公元467年
- 套用學科：數學
- 適用領域範圍：平面幾何
- 適用領域範圍：平面幾何
內容,證明,套用,
內容
在△ABC中，D是BC上的一點，連結AD。那么sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD。
逆定理： 如果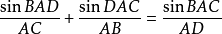
，那么B,D,C三點共線。
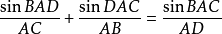
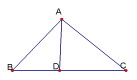張角定理定理的推論：
在定理的條件下，且∠BAD=∠CAD，即AD平分∠BAC，則B D C共線的充要條件是：2cos∠BAD/AD=1/AB+1/AC
證明
證法1：
設∠1=∠BAD，∠2=∠CAD
由分角定理，
S△ABD/S△ABC=BD/BC=(AD/AC)*(sin∠1/sin∠BAC)
→ (BD/BC)*(sin∠BAC/AD)=sin∠1/AC (1.1)
S△ACD/S△ABC=CD/BC=(AD/AB)*(sin∠2/sin∠BAC)
→ (CD/BC)*(sin∠BAC/AD)=sin∠2/AB (1.2)
(1.1)式+(1.2)式即得 sin∠1/AC+sin∠2/AB=sin∠BAC/AD。
證法2：
由正弦定理，
AD/sinB=BD/sin∠1， (2.1)
AD/sinC=CD/sin∠2， (2.2)
AB/sinC=BC/sin(∠1+∠2)， (2.3)
AC/sinB=BC/sin(∠1+∠2)； (2.4)
那么由(2.1)，(2.2)，BD=ADsin∠1/sinB，CD=ADsin∠2/sinC，從而
BC=BD+CD=AD(sin∠1/sinB+sin∠2/sinC) (2.5)
由(2.3)，(2.4)，知sin∠1/AC=sin∠1sin(∠1+∠2) / BCsinB，sin∠2/AB=sin∠2sin(∠1+∠2) / BCsinC。
將以上兩式相加，並將(2.5)代入即可。
證法3：
由面積和得：
0.5sin∠BAD*BA*AD+0.5sin∠DAC*DA*AC=0.5sin∠BAC*BA*AC
