廣義表

廣義表(Lists，又稱列表)是一種非線性的數據結構，是線性表的一種推廣。即廣義表中放鬆對表元素的原子限制，容許它們具有其自身結構。它被廣泛的套用於人工智慧等領域的表處理語言LISP語言中。在LISP語言中，廣義表是一種最基本的數據結構，就連LISP 語言的程式也表示為一系列的廣義表。

基本介紹

• 中文名：廣義表
• 外文名：Generalized table
• 性質：非線性的數據結構
• 套用於：套用於人工智慧等領域

廣義表定義

廣義表是n(n≥0)個元素a₁，a₂，…，a_i，…，a_n的有限序列。
其中：
①a_i--或者是原子或者是一個廣義表。
②廣義表通常記作：
Ls=( a₁，a₂，…，a_i，…，a_n)。
③Ls是廣義表的名字，n為它的長度。
④若a_i是廣義表，則稱它為Ls的子表。
注意：
①廣義表通常用圓括弧括起來，用逗號分隔其中的元素。
②為了區分原子和廣義表，書寫時用大寫字母表示廣義表，用小寫字母表示原子。
③若廣義表Ls非空(n≥1)，則a_l是Ls的表頭，其餘元素組成的表(a2，a3，…，a_n)稱為Ls的表尾。
④廣義表是遞歸定義的

廣義表表示

（1）廣義表常用表示
① E=()
E是一個空表，其長度為0。
② L=(a，b)
L是長度為2的廣義表，它的兩個元素都是原子，因此它是一個線性表
③ A=(x，L)=(x，(a，b))
A是長度為2的廣義表，第一個元素是原子x，第二個元素是子表L。
④ B=(A，y)=((x，(a，b))，y)
B是長度為2的廣義表，第一個元素是子表A，第二個元素是原子y。
⑤ C=(A，B)=((x，(a，b))，((x，(a，b))，y))
C的長度為2，兩個元素都是子表。
⑥ D=(a，D)=(a，(a，(a，(…))))
D的長度為2，第一個元素是原子，第二個元素是D自身，展開後它是一個無限的廣義表。

（2）廣義表的深度

一個表的"深度"是指表展開後所含括弧的層數。
【例】表L、A、B、C的深度為分別為1、2、3、4，表D的深度為∞。

（3）帶名字的廣義表表示
如果規定任何表都是有名字的，為了既表明每個表的名字，又說明它的組成，則可以在每個表的前面冠以該表的名字，於是上例中的各表又可以寫成：
①E()
②L(a，b)
③A(x，L(a，b))
④B(A(x，L(a，b))，y)
⑤C(A(x，l(a，b))，B(A(x，L(a，b))，y))
⑥D(a，D(a，D(…)))

廣義表運算

　由於廣義表是對線性表和樹的推廣，並且具有共享和遞歸特性的廣義表可以和有向圖(見第7章)建立對應，因此廣義表的大部分運算與這些數據結構上的運算類似。　　在此，只討論廣義表的兩個特殊的基本運算：取表頭head(Ls)和取表尾tail(Ls)。　　根據表頭、表尾的定義可知：任何一個非空廣義表的表頭是表中第一個元素，它可以是原子，也可以是子表，而其表尾必定是子表。　　【例】　　head(L)=a， tail(L)=(b)　　head(B)=A， tail(B)=(y)　　由於tail(L)是非空表，可繼續分解得到：　　head(tail(L))=b， tail(tail(L))=()　　對非空表A和(y)，也可繼續分解。　　注意:廣義表()和(())不同。前者是長度為0的空表，對其不能做求表頭和表尾的運算；而後者是長度為l的非空表(只不過該表中惟一的一個元素是空表)，對其可進行分解，得到的表頭和表尾均是空表()。

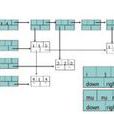
頭尾鍊表存儲結構

typedef enum {ATOM, LIST} ElemTag; /* ATOM=0，表示原子；LIST=1，表示子表*/

typedef struct GLNode

{

ElemTag tag; /*標誌位tag用來區別原子結點和表結點*/

union

{

AtomType atom; /*原子結點的值域atom*/

struct { struct GLNode * hp, *tp;} htp; /*表結點的指針域htp， 包括

表頭指針域hp和表尾指針域tp*/

} atom_htp; /* atom_htp 是原子結點的值域atom和

表結點的指針域htp的聯合體域*/

} *GList；

擴展線性存儲

typedef enum {ATOM,LIST} ElemTag;

typedef struct GLNode

{ELemTag tag;

union

{AtomType atom;

struct GLNode *hp;

}

struct GLNode *ht;

}*GList;