欒茂田等從更加廣泛得多的基礎上提出了一種用於非均質堤壩穩定分析的廣義極限平衡法；可以計算不同參數(土坡面幾何形狀、土料強度特性和地震荷載)組合下的潛在滑動體及相應的臨界地震荷載。這一方法的原理是將傳統的極限平衡法與Lagrange不定乘子法有機結合，據此進行了大量算例計算和分析。
基本介紹
- 中文名：廣義極限平衡法
- 外文名：general limit equilibrium method
- 所屬領域：數理科學
- 提出者：欒茂田等
- 性質：極限分析方法
定義,相關結論,
定義
廣義極限平衡法(general limit equilibrium method)考慮了其他各種方法涉及的關鍵因素，它是基於兩個平衡方程得出的安全係數。一個安全係數由力矩平衡給出，另一個由水平方向力平衡給出，並且允許條帶間法向力和切向力的變化。廣義極限平衡法採用Morgenstern和Price在1965年提出的下面公式來處理條帶間的剪力假定問題：
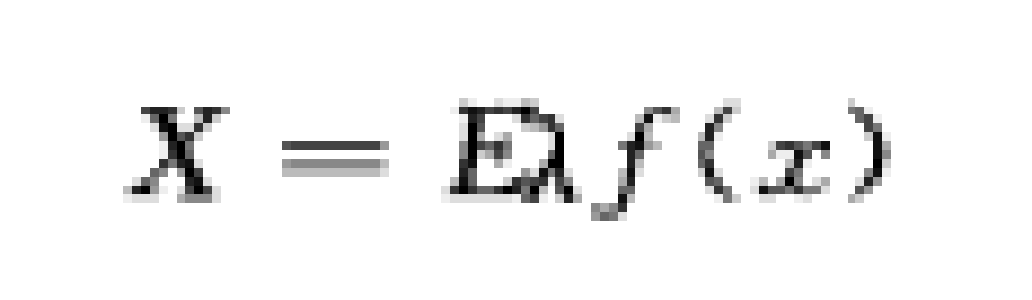1式中，f(x)為任意函式；E為條帶間法向應力；λ為函式使用百分比。
廣義極限平衡法通過力矩平衡計算安全係數，公式為
2通過水平力平衡得出的安全係數為
3式中，c'為有效粘聚力；
為有效內摩擦角；U為孔隙水壓力；N為條帶底部法向力；W為條帶重量；D為線荷載；α為條帶底部傾角；ψ為外荷載與垂直方向夾角。
相關結論
(i)無粘性土壩發生壩坡失穩的最可能形式是淺層平面滑動，其水平屈服地震係數為
=tg(Φ一β)，這裡Φ為土的內摩擦角，β為坡角。
(ii)粘性土壩的粘結力，包括自身的內粘結力和含水時毛細作用形成的表面粘結力，顯著地提高了壩坡上各部位尤其是壩頂附近的潛在滑動體的極限抗震能力。
(iii)將粘結力歸一化為
=c/γH，其中γ為土的重度，H為離壩頂深度。根據一般規律，可設c在壩體中從壩頂向下線性增大，而 則隨H的變小(滑動體滑出點接近壩頂，即滑出點深度Hs減小)而增大。根據這一規律求得的屈服加速度係數 隨滑動體深度而變化的規律，如圖4所示例的那樣變化。這是均質壩坡，坡比1：2，土質強度指標為Φ=30°，c/γHd=0．0125，Hd為壩高。其他情況的類似的 -y/Hd關係均可按公式算得。由圖可知粘性土壩壩頂處 非常大(理論上趨於無窮大)，即使反應加速度很大，也不致發生近壩頂處的淺層滑動。這和無粘性土壩不同。砂質土壩和堆石壩的屈服加速度沿壩高大致均勻分布，壩頂附近極易因較大慣性力作用而發生局部顆粒滾動、剝落或部分土體淺層滑移。
4
4(iv)隨著c或Φ的增大圖5、坡角的減小、壩高Hd的降低， 都將有較明顯的增大。
(v)同一壩坡的不同滑出點的滑動體，其起始滑動點總是在壩頂或在另一坡面的某一位置處。這一位置似乎與滑動體貫穿的深度無關。
5
5其次，欒茂田等將用於估算潛在滑動體的平均地震反應加速度的一維剪下梁法加以修改和發展，使其適用於壩體材料的剪下模量按指數規律變化、壩體與壩基覆蓋層有不同材料性質等情況，並且對滑動體的形狀也按上述廣義極限平衡法解得的“真實”滑動面來確定。通過對算例所得數據的分析，得出一些有用的結果.
計算結果表明：輸入Elcentro地震動記錄時，各潛在滑動體上平均地震係數與土壩壩體(按一維計算)地震係數的頻率特性相差不大。當壩體第1自振周期T1較小，尤其當T1在地震卓越周期Te附近時，自壩頂或另一壩坡上部開始而貫穿某一深度滑出的滯動體上的平均地震係數
大於相應深度處壩體最大絕對加速度係數。當T1較大時，情況恰好相反。
選擇實際工程中常見的參數範圍，如坡比為1：1.5，1：2,1：2.5，阻尼比為10%～20%，並改變模量與壩高，進行數值計算。壩體第1自振周期T1範圍為0.15～3.1s．圖6列出了T1/Te
在三個不同範圍內，即T1/Te>3，0.5<T1/Te<3和T1/Te<0.5時， /
值沿高度的變化。這裡 為滑出點高度不同的滑動體上最大平均反應加速度係數， 為壩頂最大加速度。圖中所示的是阻尼比20%的情況。圖上所畫實線是這三個頻率比範圍內所得數據的平均值。為比較起見，圖上還用虛線畫出了Makdisi和Seed的類似計算結果。計算結果表明，Makdisi和Seed的單純圓弧滑動面求得的 似乎總是偏小，並且 只依賴於滑動面所貫穿的最大深度(y/Hd)，而與壩頓和材料強度無關，這也似乎是不符實際的．
6欒茂田等提出的土壩地震永久變形的計算圖式如圖9所示。廣義極限平衡法證明粘性土壩的臨界破壞機制(滑動方式)為沿對數螺線柱面的轉動。為簡化計算，假定有效水平地震慣性力k(t)W作用在滑動體的質心處，滑動體作剛性轉動的動力平衡方程可列為
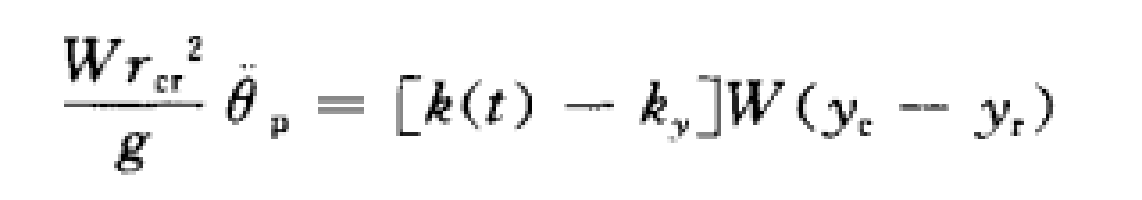7式中W——滑動體重量；
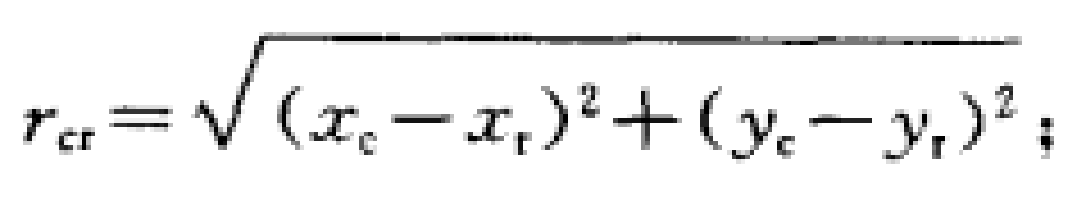8(xc，yc)——滑動體質心c的坐標；
(xr，yr)——滑動中心o'的坐標；
經簡化後，得
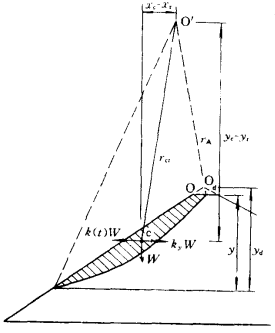9
9
10令xp、yp分別表示滑動體質心處的水平和豎向剛體位移值，則
11按Newmark理論，k(t)< 時，滑動體不發生運動。k(t)= 為臨界狀態;k(t)> 則發生運動。滑動體位移量取決於(k一 )的幅值及脈衝的持續時間。滑動至相對運動速度為零時停止。對(10)式進行二次積分即可求得每一脈衝中產生的位移量。將一次地震過程中各脈衝引起的位移累加，即得到該次地震中該滑動體產生的永久變形。這裡假定振動過程中土的強度無顯著損失，並近似地認為壩坡屈服加速度係數不隨時間變化。圖12給出了一個壩坡幾個滑動體的地震水平永久位移xp發展過程。
12
12