在矩陣運算中,該矩陣有特徵值是重根,則該特徵值所對應的特徵向量所構成空間(即特徵子空間,也是方程組(λI-A)x=0)的維數,稱為幾何重數。
基本介紹
- 中文名:幾何重數
- 外文名:geometric multiplicity
- 套用領域:矩陣分析
- 含義:特徵值對應的特徵子空間的維數
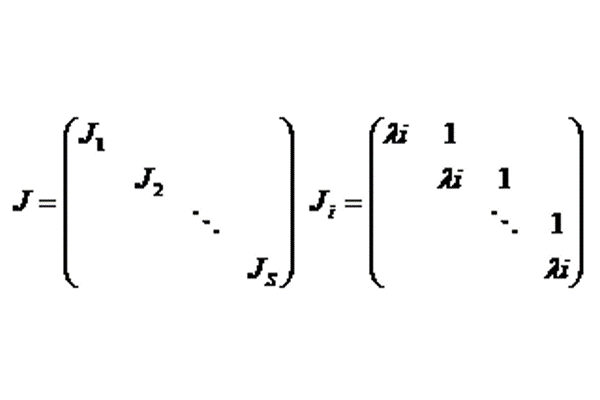
在矩陣運算中,該矩陣有特徵值是重根,則該特徵值所對應的特徵向量所構成空間(即特徵子空間,也是方程組(λI-A)x=0)的維數,稱為幾何重數。
在矩陣運算中,該矩陣有特徵值是重根,則該特徵值所對應的特徵向量所構成空間(即特徵子空間,也是方程組(λI-A)x=0)的維數,稱為幾何重數。...
重數,數學名詞,包括幾何重數和代數重數。在矩陣運算中,該矩陣有特徵值是重根,則該特徵值所對應的特徵向量所構成空間的維數,稱為幾何重數。(舉例:一條直線與...
矩陣J的特徵值(計入重數)就是主對角線上的係數。 對於J的一個特徵值,它的幾何重數就是屬於特徵值的若爾當塊的個數。 所有屬於特徵值的若爾當塊的維數之和...
中的重數 稱為 的代數重數,特徵子空間 的維數 稱為 幾何重數,每個特徵值 的幾何重數≥1且≤代數重數。可對角化 所有的特徵值的幾何重數等於代數重數。特殊...
特徵向量的極大線性無關向量組中向量的個數可以由所有特徵值的幾何重數之和來確定。 [1] 特徵分解分解方法 編輯 特徵分解矩陣的特徵分解 ...
在任一基下矩陣的特徵多項式)的根均屬於P,且各特徵值的幾何重數等於代數重數。[4] n階矩陣A與對角陣相似問題1)如果A有n個線性無關的特徵向量,則A與對角陣...
4.如果A。的實部為零的特徵值的代數重數都等於其幾何重數而其餘特徵值皆具有負實部,則系統(1)是臨界穩定的,否則是不穩定的.[1] ...
3.3.2 特徵值的代數重數和幾何重數3.3.3 矩陣Jordan標準形§3.4 方陣的最小多項式3.4.1 方陣的化零多項式3.4.2 最小多項式3.4.3 最小多項式與方陣...
三、代數重數與幾何重數四、擾動法7.4 線性變換(矩陣)的對角化問題(Ⅰ)一、利用特徵向量判定二、利用特徵值判定7.5 不變子空間一、不變子空間的判定...
有一個正實部的根,則系統不穩定;實部為零的根代數重數等於其幾何重數且其餘根均有負實部,則屬臨界情況;實部為零的重根代數重數大於幾何重數,則系統不穩定...
