平面對偶圖(dual graph)一類特殊的圖。指由一個平面圖派生出的另一平面圖。
基本介紹
- 中文名:平面對偶圖
- 外文名:dual graph
在平面圖G的每個面內選取一點作為頂點,對於G的任一條邊。,將與其相鄰的兩個面內的頂點用一條僅與‘有一交點且不與圖G的其他任何邊相交的簡單曲線連結,這樣得到的平面圖稱為G的平面對偶圖,記為G‘.亦稱G’為G的幾何對偶.平面對偶具有對稱性,即,若G‘為G的平面對偶圖,則G亦為G‘的平面對偶圖.附圖中的實線和虛線分別代表互為對偶的兩個平面圖.若圖G和G’的邊集間可建立一個一一對應,使得任何一對對應邊集E,和E;有以下關係:
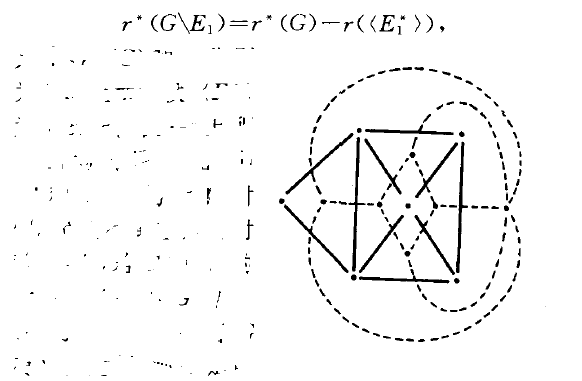
平面對偶圖
其中,r ` (G)和r分別為圖的上秩和秩,(E扮為邊集E1.在G‘上所導出的支撐子圖,則G‘稱為G的代數對偶.代數對偶也具有對稱性,即,若G’為G的代數對偶,則G也為G‘的代數對偶.若G有平面對偶,則G是可平面的.反之,任何可平面的圖也必有代數對偶.這就是惠特尼定理,它是由美國數學家惠特尼(Whit-ney , H.)於1933年首先發現的.這個定理使人們可以不必區別可平面圖的幾何對偶與代數對偶.若G的平面對偶G‘與G本身同構,則稱G為自對偶圖.
