帶邊Ck流形（Ck manifold with boundry）是一種有邊緣的Ck類?>微分流形。
基本介紹
- 中文名：帶邊Ck流形
- 外文名：Ck manifold with boundry
- 適用範圍：數理科學
簡介,性質,微分流形,
簡介
帶邊Ck流形是一種有邊緣的Ck類微分流形。
設M是一個仿緊豪斯多夫空間，{(Ui,𝜙i)|i∈I}是一個圖冊，其中Ui是M中的開集，𝜙i是Ui到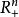
的一個開集上的同胚，使得當Ui∩Uj≠∅時，映射
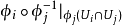是Ck類的，且至少有一個U，使得𝜙i(Ui)∩Rn-1≠∅（其中Rn-1是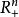的邊界），則稱這個圖冊定義M為一個帶邊Ck流形。
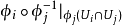
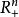
性質
Ck流形中的流形也稱為無邊Ck流形。流形是否帶邊是一個拓撲性質，與微分結構𝓕={(Ui,𝜙i)|i∈I}的選取無關。
由定義易知n維球體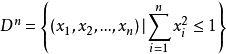
在通常拓撲之下為Ck流形。
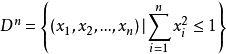
微分流形
（differentiable manifold）
微分流形，也稱為光滑流形（smooth manifold），是拓撲學和幾何學中一類重要的空間，是帶有微分結構的拓撲流形。
微分流形是微分幾何與微分拓撲的主要研究對象，是三維歐式空間中曲線和曲面概念的推廣，可以有更高的維數，而不必有距離和度量的概念。
