帶調和函式(zonal harmonic function)一類具有特殊性質的球面調和函式.由等式
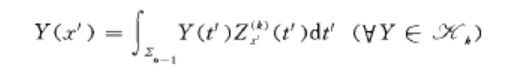
確定的k次球面調和函式Z歲t')稱為以x'為極點的k次帶調和函式，其中交飛為k次球面調和函式類.Z歲 }t})的一個重要特性就是:對任一旋轉P，有
帶調和函式
相關詞條
- 帶調和函式
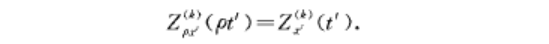
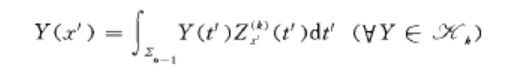
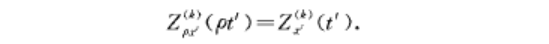
帶調和函式(zonal harmonic function)一類具有特殊性質的球面調和函式.由等式 確定的k次球面調和函式Z歲t')稱為以x'為極點的k次帶調和函式,其中交飛為k次球面...
- 調和函式
調和函式是在某區域中滿足拉普拉斯方程的函式。通常對函式本身還附加一些光滑性條件,例如有連續的一階和二階偏導數。當自變數為n個(從而區域是n維的)時,則稱它為...
- 面調和函式
面調和函式(surface harmonics)有時亦稱球函式.即拉普拉斯方程齊次多項式解的角向部分.將拉普拉斯方程在球坐標系((r, B,卯下的解寫成r'Y (B,卯的形式((n為正...
- 球函式
球函式(spherical function)通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程...
- 調和山脈
這兩類山脈的成生,前者可以用某種帶調和函式說明,後者可以用某種縱調和函式來論證,因此稱為調和山脈。早先,以研究潮汐著名的力學家達爾文曾從理論方面論及地殼表面...
- 帶球函式
帶球函式(zonal harmonic function)又稱帶調和函式。球函式的一種。若它是n級的,則它在球面上n個不同緯度處的值等於零;在球面其餘區域,它或取正值或取負值,...
- 蓋爾范德
論文涉及的領域也十分廣泛,包括巴拿赫代數、調和分析、群表示論、積分幾何、廣義函式、無窮維李代數的上同調、微分方程、生物學和生理學。 蓋爾范德又譯為蓋爾芳特,...
- 位勢論
位勢論是數學的一支,它可以定義為調和函式的研究。“位勢論”一詞的來源在於,在19世紀的物理學中,自然界的基本力被相信為從滿足拉普拉斯方程的位勢導出。因此,...
