鄰接矩陣(Adjacency Matrix):是表示頂點之間相鄰關係的矩陣。設G=(V,E)是一個圖,其中V={v1,v2,…,vn}。G的鄰接矩陣是一個具有下列性質的n階方陣
基本介紹
- 中文名:帶權鄰接矩陣
- 外文名:Adjacency Matrix)
- 涉及學科:數學
- 釋義:專業名詞
定義,特點,鄰接矩陣的C語言描述,圖的鄰接矩陣表示法,鄰接矩陣(adjacency matrix)的Matlab表達,
定義
鄰接矩陣(Adjacency Matrix):是表示頂點之間相鄰關係的矩陣。設G=(V,E)是一個圖,其中V={v1,v2,…,vn}。G的鄰接矩陣是一個具有下列性質的n階方陣:
①對無向圖而言,鄰接矩陣一定是對稱的,而且對角線一定為零,有向圖則不一定如此。
②在無向圖中,任一頂點i的度為第i列所有元素的和,在有向圖中頂點i的出度為第i行所有元素的和,而入度為第i列所有元素的和。
③用鄰接矩陣法表示圖共需要n^2個空間,由於無向圖的鄰接矩陣一定具有對稱關係,所以扣除對角線為零外,僅需要存儲上三角形或下三角形的數據即可,因此僅需要n(n-1)/2個空間。
特點
無向圖的鄰接矩陣一定是對稱的,而有向圖的鄰接矩陣不一定對稱。因此,用鄰接矩陣來表示一個具有n個頂點的有向圖時需要n^2個單元來存儲鄰接矩陣;對有n個頂點的無向圖則只存入上(下)三角陣中剔除了左上右下對角線上的0元素後剩餘的元素,故只需1+2+...+(n-1)=n(n-1)/2個單元。
無向圖鄰接矩陣的第i行(或第i列)非零元素的個數正好是第i個頂點的度。
有向圖鄰接矩陣中第i行非零元素的個數為第i個頂點的出度,第i列非零元素的個數為第i個頂點的入度,第i個頂點的度為第i行與第i列非零元素個數之和。
用鄰接矩陣表示圖,很容易確定圖中任意兩個頂點是否有邊相連。
鄰接矩陣的C語言描述
用一個順序表來存儲頂點信息

int i,j,k,w;
scanf("%d%d",&G->n,&G->e); //輸入頂點數和邊數
for(i = 0;i < n;i++) //讀人頂點信息,建立頂點表
{
G->vexs=getchar();
}
for(i = 0;i < n;i++)
{
for(j = 0;j < n;j++)
{
G->edges[j] = 0; //鄰接矩陣初始化
}
}
for(k = 0;k < e;k++)
{//讀入e條邊,建立鄰接矩陣
scanf("%d%d%d",&i,&j,&w); //輸入邊(v i ,v j )上的權w
G->edges[j]=w;
G->edges[j]=w;
}
}//CreateMGraph
圖的鄰接矩陣表示法
1.圖的鄰接矩陣表示法
在圖的鄰接矩陣表示法中:
① 用鄰接矩陣表示頂點間的相鄰關係
② 用一個順序表來存儲頂點信息
2.圖的鄰接矩陣(Adjacency Matrix)
設G=(V,E)是具有n個頂點的圖,則G的鄰接矩陣是具有如下性質的n階方陣:
【例】下圖中無向圖G 5 和有向圖G 6 的鄰接矩陣分別為A l 和A 2 。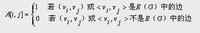
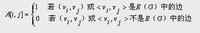
3.網路的鄰接矩陣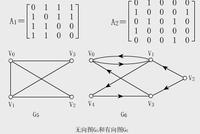

若G是網路,則鄰接矩陣可定義為:
其中: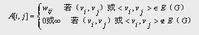
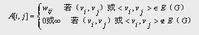
w ij 表示邊上的權值;
∞表示一個計算機允許的、大於所有邊上權值的數。
【例】下面帶權圖的兩種鄰接矩陣分別為A 3 和A 4 。
4.圖的鄰接矩陣存儲結構形式說明

#define MaxVertexNum l00 //最大頂點數,應由用戶定義
typedef char VertexType; //頂點類型應由用戶定義
typedef int EdgeType; //邊上的權值類型應由用戶定義
typedef struct{
VextexType vexs[MaxVertexNum] //頂點表
EdeType edges[MaxVertexNum][MaxVertexNum];
//鄰接矩陣,可看作邊表
int n,e; //圖中當前的頂點數和邊數
}MGragh;
注意:
① 在簡單套用中,可直接用二維數組作為圖的鄰接矩陣(頂點表及頂點數等均可省略)。
② 當鄰接矩陣中的元素僅表示相應的邊是否存在時,EdgeTyPe可定義為值為0和1的枚舉類型。
③ 無向圖的鄰接矩陣是對稱矩陣,對規模特大的鄰接矩陣可壓縮存儲。
④ 鄰接矩陣表示法的空間複雜度S(n)=0(n 2 )。
5.建立無向網路的算法。
void CreateMGraph(MGraph *G)
{//建立無向網的鄰接矩陣表示
int i,j,k,w;
scanf("%d%d",&G->n,&G->e); //輸入頂點數和邊數
for(i = 0;i < n;i++) //讀人頂點信息,建立頂點表
{
G->vexs=getchar();
}
for(i = 0;i < n;i++)
{
for(j = 0;j < n;j++)
{
G->edges[j] = 0; //鄰接矩陣初始化
}
}
for(k = 0;k < e;k++)
{//讀入e條邊,建立鄰接矩陣
scanf("%d%d%d",&i,&j,&w); //輸入邊(v i ,v j )上的權w
G->edges[j]=w;
G->edges[j]=w;
}
}//CreateMGraph
該算法的執行時間是0(n+n 2 +e)。由於e
根據圖的定義可知,圖的邏輯結構分為兩部分:V和E的集合。因此,用一個一維數組存放圖中所有頂點數據;用一個二維數組存放頂點間關係(邊或弧)的數據,稱這個二維數組為鄰接矩陣。鄰接矩陣又分為有向圖鄰接矩陣和無向圖鄰接矩陣。
鄰接矩陣(adjacency matrix)的Matlab表達
N = 4; //圖中的節點數目
dag = zeros(N,N);//鄰接矩陣初始化,值均為0
C = 1; S = 2; R = 3; W = 4;//制定各節點編號
dag(C,[R S]) = 1;//有兩條有向邊:C->R,C->S
dag(R,W) = 1;//有向邊:R->W
dag(S,W)=1;//有向邊:S->W
